2022年秋季湘教版数学九年级上册第二章《一元二次方程》单元检测B

试卷更新日期：2022-10-05 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 一元二次方程 $2 x^{2} + x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
2. 若关于 $x$ 的一元二次方程 $x^{2} - a x + 6 = 0$ 的一个根是2，则 $a$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
3. 已知关于x的一元二次方程（m﹣1）x²+2x﹣3＝0有实数根，则m的取值范围是（）

A、m≥ $\frac{2}{3}$ B、m＜ $\frac{2}{3}$ C、m＞ $\frac{2}{3}$ 且m≠1 D、m≥ $\frac{2}{3}$ 且m≠1

查看试题解析
4. 定义新运算 $a * b$ ：对于任意实数 $a$ ， $b$ 满足 $a * b = (a + b) (a - b) - 1$ ，其中等式右边是通常的加法、减法、乘法运算，例如 $3 * 2 = (3 + 2) (3 - 2) - 1 = 5 - 1 = 4$ ．若 $x * k = 2 x$ （ $k$ 为实数）是关于 $x$ 的方程，则它的根的情况是（）

A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根

查看试题解析
5. 下列说法正确的是（）
①若二次根式 $\sqrt{1 - x}$ 有意义，则x的取值范围是x≥1．
②7＜ $\sqrt{65}$ ＜8．
③若一个多边形的内角和是540°，则它的边数是5．
④ $\sqrt{16}$ 的平方根是±4．
⑤一元二次方程x²﹣x﹣4＝0有两个不相等的实数根．

A、①③⑤ B、③⑤ C、③④⑤ D、①②④

查看试题解析
6. 某种商品原来每件售价为150元，经过连续两次降价后，该种商品每件售价为96元，设平均每次降价的百分率为x，根据随意，所列方程正确的是（）

A、 $150 (1 - x^{2}) = 96$ B、 $150 (1 - x) = 96$ C、 $150 (1 - x)^{2} = 96$ D、 $150 (1 - 2 x) = 96$

查看试题解析
7. 已知一元二次方程式 $(x - 2)^{2} = 3$ 的两根为 $a$ 、 $b$ ，且 $a > b$ ，求 $2 a + b$ 之值为何？（）

A、9 B、-3 C、 $6 + \sqrt{3}$ D、 $- 6 + \sqrt{3}$

查看试题解析
8. 已知 $m$ 、 $n$ 是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 2 m$ 的值为（）

A、0 B、-10 C、3 D、10

查看试题解析
9. 已知关于x的一元二次方程 $x^{2} - m n x + m + n = 0$ ，其中m ， n在数轴上的对应点如图所示，则这个方程的根的情况是（）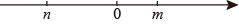

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
10. 在平面直角坐标系中，若直线 $y = - x + m$ 不经过第一象限，则关于 $x$ 的方程 $m x^{2} + x + 1 = 0$ 的实数根的个数为（）

A、0个 B、1个 C、2个 D、1或2个

查看试题解析

二、填空题（每题3分，共18分）

11. 若一元二次方程 $x^{2} - 4 x + 3 = 0$ 的两个根是 $x_{1}$ ， $x_{2}$ ，则 $x_{1} \cdot x_{2}$ 的值是.

查看试题解析
12. 若a是一元二次方程 $x^{2} + 2 x - 3 = 0$ 的一个根，则 $2 a^{2} + 4 a$ 的值是．

查看试题解析
13. 若m，n是一元二次方程 $x^{2} + 3 x - 1 = 0$ 的两个实数根，则 $\frac{m^{3} + m^{2} n}{3 m - 1}$ 的值为.

查看试题解析
14. 已知关于 $x$ 的方程 $x^{2} - (k + 4) x + 4 k = 0$ （ $k \neq 0$ ）的两实数根为 $x_{1}$ ， $x_{2}$ ，若 $\frac{2}{x_{1}} + \frac{2}{x_{2}} = 3$ ，则 $k =$ .

查看试题解析
15. 若等腰三角形的一边长是4，另两边的长是关于 $x$ 的方程 $x^{2} - 6 x + n = 0$ 的两个根，则 $n$ 的值为．

查看试题解析
16. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - a = 0$ ，有下列结论：
①当 $a > - 1$ 时，方程有两个不相等的实根；

②当 $a > 0$ 时，方程不可能有两个异号的实根；

③当 $a > - 1$ 时，方程的两个实根不可能都小于1；

④当 $a > 3$ 时，方程的两个实根一个大于3，另一个小于3．

以上4个结论中，正确的个数为．

查看试题解析

三、解答题（共9题，共72分）

17. 解方程：2（x﹣3）=3x（x﹣3）．

查看试题解析
18. 解方程： $3 x^{2} - 2 x - 2 = 0$ ．

查看试题解析
19. 在平面直角坐标系中，如果一个点的横坐标与纵坐标互为相反数，则称该点为“黎点”.例如（﹣1，1），（2022，﹣2022）都是“黎点”.

(1)、求双曲线y＝ $\frac{- 9}{x}$ 上的“黎点”；

(2)、若抛物线y＝ax²﹣7x+c（a、c为常数）上有且只有一个“黎点”，当a＞1时，求c的取值范围.

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - 4 x - 2 m + 5 = 0$ 有两个不相等的实数根.

(1)、求实数m的取值范围；

(2)、若该方程的两个根都是符号相同的整数，求整数m的值.

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 m x + 3 m^{2} = 0$ ．

(1)、求证：该方程总有两个实数根；

(2)、若 $m > 0$ ，且该方程的两个实数根的差为2，求 $m$ 的值．

查看试题解析
22. 某养殖场为了响应党中央的扶贫政策，今年起采用“场内+农户”养殖模式，同时加强对蛋鸡的科学管理，蛋鸡的产蛋率不断提高，三月份和五月份的产蛋量分别是2.5万kg与3.6万kg，现假定该养殖场蛋鸡产蛋量的月增长率相同.

(1)、求该养殖场蛋鸡产蛋量的月平均增长率；

(2)、假定当月产的鸡蛋当月在各销售点全部销售出去，且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务，那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点？

查看试题解析
23. 一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

(1)、若降价3元，则平均每天销售数量为件；

(2)、当每件商品降价多少元时，该商店每天销售利润为1200元？

查看试题解析
24. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x + k + 2 = 0$ 的两个实数根．

(1)、求k的取值范围；

(2)、是否存在实数k，使得等式 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = k - 2$ 成立？如果存在，请求出k的值，如果不存在，请说明理由．

查看试题解析
25. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如下表:
X(元)
15
20
30
…
y(袋)
25
20
10
…
若日销售量y是销售价x的一次函数,试求:

(1)、日销售量y(袋)与销售价x(元)的函数关系式;

(2)、假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?

查看试题解析

X(元)	15	20	30	…
y(袋)	25	20	10	…

2022年秋季湘教版数学九年级上册第二章 《一元二次方程》单元检测B

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

2022年秋季湘教版数学九年级上册第二章《一元二次方程》单元检测B