2022年秋季湘教版数学九年级上册第二章《一元二次方程》单元检测A

试卷更新日期：2022-10-04 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 一元二次方程 $x^{2} + 4 x - 8 = 0$ 的解是（）

A、 $x_{1} = 2 + 2 \sqrt{3} ， x_{2} = 2 - 2 \sqrt{3}$ B、 $x_{1} = 2 + 2 \sqrt{2} ， x_{2} = 2 - 2 \sqrt{2}$ C、 $x_{1} = - 2 + 2 \sqrt{2} ， x_{2} = - 2 - 2 \sqrt{2}$ D、 $x_{1} = - 2 + 2 \sqrt{3} ， x_{2} = - 2 - 2 \sqrt{3}$

查看试题解析
2. 下列一元二次方程有实数解的是（）

A、2x²﹣x+1＝0 B、x²﹣2x+2＝0 C、x²+3x﹣2＝0 D、x²+2＝0

查看试题解析
3. 若 $x = - 2$ 是一元二次方程 $x^{2} + 2 x + m = 0$ 的一个根，则方程的另一个根及m的值分别是（）

A、0，-2 B、0，0 C、-2，-2 D、-2，0

查看试题解析
4. 对于实数 $a$ ， $b$ 定义新运算： $a ※ b = a b^{2} - b$ ，若关于 $x$ 的方程 $1 ※ x = k$ 有两个不相等的实数根，则 $k$ 的取值范围（）

A、 $k > - \frac{1}{4}$ B、 $k < - \frac{1}{4}$ C、 $k > - \frac{1}{4}$ 且 $k \neq 0$ D、 $k \geq - \frac{1}{4}$ 且 $k \neq 0$

查看试题解析
5. 已知关于 $x$ 的方程 $x^{2} - (2 m - 1) x + m^{2} = 0$ 的两实数根为 $x_{1}$ ， $x_{2}$ ，若 $(x_{1} + 1) (x_{2} + 1) = 3$ ，则 $m$ 的值为（）

A、-3 B、-1 C、-3或3 D、-1或3

查看试题解析
6. 关于x的一元二次方程 $3 x^{2} - 2 x + m = 0$ 有两根，其中一根为 $x = 1$ ，则这两根之积为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、1 D、 $- \frac{1}{3}$

查看试题解析
7. 已知一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1}^{2} - 5 x_{1} - 2 x_{2}$ 的值为（）

A、-7 B、-3 C、2 D、5

查看试题解析
8. 关于x的方程 $(x - 1) (x + 2) = ρ^{2}$ （ $ρ$ 为常数）根的情况下，下列结论中正确的是（）

A、两个正根 B、两个负根 C、一个正根，一个负根 D、无实数根

查看试题解析
9. 某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为（）

A、30（1+x）²＝50 B、30（1﹣x）²＝50 C、30（1+x²）＝50 D、30（1﹣x²）＝50

查看试题解析
10. 有一个人患了流行性感冒，经过两轮传染后共有144人患了流行性感冒，则每轮传染中平均一个人传染的人数是（）

A、14 B、11 C、10 D、9

查看试题解析

二、填空题（每题3分，共18分）

11. 关于x的一元二次方程 $(k - 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则k的取值范围是．

查看试题解析
12. 一元二次方程 $(x - 2) (x + 7) = 0$ 的根是.

查看试题解析
13. $α$ 、 $β$ 是关于 $x$ 的方程 $x^{2} - x + k - 1 = 0$ 的两个实数根，且 $α^{2} - 2 α - β = 4$ ，则 $k$ 的值为．

查看试题解析
14. 已知x₁、x₂是关于x的方程x²﹣2x+k﹣1＝0的两实数根，且 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ ＝x₁²+2x₂﹣1，则k的值为 .

查看试题解析
15. 我国南宋数学家杨辉所著《田亩比类乘除算法》中记载了这样一道题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步。”其大意为：一个矩形的面积为864平方步，宽比长少12步，问宽和长各多少步？设矩形的宽为x步，根据题意，可列方程为。

查看试题解析
16. 为增强学生身体素质，提高学生足球运动竞技水平，我市开展“市长杯”足球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应邀请多少个球队参赛？设邀请x个球队参赛，根据题意，可列方程为．

查看试题解析

三、解答题（共9题，共72分）

17. 解方程： $(2 x + 3)^{2} = (3 x + 2)^{2}$

查看试题解析
18. 用配方法求一元二次方程 $(2 x + 3) (x - 6) ＝ 16$ 的实数根．

查看试题解析
19. 解方程：2（x﹣3）=3x（x﹣3）．

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - 3 m^{2} = 0$ .

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根分别为 $α$ ， $β$ ，且 $α + 2 β = 5$ ，求 $m$ 的值.

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} + 1 = 0$ 有两个不等实数根 $x_{1}$ ， $x_{2}$ .

(1)、求k的取值范围；

(2)、若 $x_{1} x_{2} = 5$ ，求k的值.

查看试题解析
22. 安顺市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量y（千元）与每千元降价x（元）（0<x<20）之间满足一次函数关系，其图象如图所示：

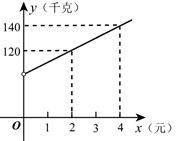(1)、求y与x之间的函数关系式；

(2)、商贸公司要想获利2090元，则这种干果每千克应降价多少元？

查看试题解析
23. 已知关于x的一元二次方程 $x^{2} - 6 x + 2 m - 1 = 0$ 有 $x_{1}$ ， $x_{2}$ 两实数根.

(1)、若 $x_{1} = 1$ ，求 $x_{2}$ 及 $m$ 的值；

(2)、是否存在实数 $m$ ，满足 $(x_{1} - 1) (x_{2} - 1) = \frac{6}{m - 5}$ ？若存在，求出求实数 $m$ 的值；若不存在，请说明理由.

查看试题解析
24. 某造纸厂为节约木材，实现企业绿色低碳发展，通过技术改造升级，使再生纸项目的生产规模不断扩大.该厂3，4月份共生产再生纸800吨，其中4月份再生纸产量是3月份的2倍少100吨.

(1)、求4月份再生纸的产量；

(2)、若4月份每吨再生纸的利润为1000元，5月份再生纸产量比上月增加 $m %$ .5月份每吨再生纸的利润比上月增加 $\frac{m}{2} %$ ，则5月份再生纸项目月利润达到66万元.求 $m$ 的值；

(3)、若4月份每吨再生纸的利润为1200元，4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同，6月份再生纸项目月利润比上月增加了 $2 5%$ .求6月份每吨再生纸的利润是多少元？

查看试题解析
25. 阅读理解：
材料一：若三个非零实数x ， y ， z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实教x ， y ， z构成“和谐三数组”.

材料二：若关于x的一元二次方程ax²+bx +c= 0(a≠0)的两根分别为 $x_{1}$ ， $x_{2}$ ，则有 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a}$ ．

问题解决：

(1)、请你写出三个能构成“和谐三数组”的实数；

(2)、若 $x_{1}$ ， $x_{2}$ 是关于x的方程ax²+bx +c= 0 (a ， b ， c均不为0)的两根， $x_{3}$ 是关于x的方程bx+c=0(b ， c均不为0)的解．求证：x₁ ，x₂ ， x₃可以构成“和谐三数组”；

(3)、若A(m ， y₁) ，B(m + 1，y₂) ，C(m+3，y₃)三个点均在反比例函数 $y = \frac{4}{x}$ 的图象上，且三点的纵坐标恰好构成“和谐三数组”，求实数m的值．

查看试题解析

2022年秋季湘教版数学九年级上册第二章 《一元二次方程》单元检测A

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

2022年秋季湘教版数学九年级上册第二章《一元二次方程》单元检测A