2022年秋季北师版数学九年级上册第二章《一元二次方程》单元检测B

试卷更新日期：2022-10-04 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 把一元二次方程 $x (2 x - 1) = x - 3$ 化为一般形式，正确的是（）

A、 $2 x^{2} + 3 = 0$ B、 $2 x^{2} - 2 x - 3 = 0$ C、 $2 x^{2} - x + 2 = 0$ D、 $2 x^{2} - 2 x + 3 = 0$

查看试题解析
2. 根据方程x²﹣3x﹣5＝0可列表如下（　　）
x
﹣3
﹣2
﹣1
…
4
5
6
x²﹣3x﹣5
13
5
﹣1
…
﹣1
5
13
则x的取值范围是（　　）

A、﹣3＜x＜﹣2或4＜x＜5 B、﹣2＜x＜﹣1或5＜x＜6 C、﹣3＜x＜﹣2或5＜x＜6 D、﹣2＜x＜﹣1或4＜x＜5

查看试题解析
3. 若关于x的一元二次方程x²+6x+c＝0配方后得到方程（x+3）²＝2c，则c的值为（　　）

A、﹣3 B、0 C、3 D、9

查看试题解析
4. 将关于x的一元二次方程 $x^{2} - p x + q = 0$ 变形为 $x^{2} = p x - q$ ，就可以将 $x^{2}$ 表示为关于x的一次多项式，从而达到“降次”的目的，又如 $x^{3} = x \cdot x^{2} = x (p x - q) =$ …，我们将这种方法称为“降次法”，通过这种方法可以化简次数较高的代数式.根据“降次法”，已知： $x^{2} - x - 1 = 0$ ，且 $x > 0$ ，则 $x^{4} - 2 x^{3} + 3 x$ 的值为（）

A、 $1 - \sqrt{5}$ B、 $3 - \sqrt{5}$ C、 $1 + \sqrt{5}$ D、 $3 + \sqrt{5}$

查看试题解析
5. 若直角三角形的两边长分别是方程 $x^{2} - 7 x + 12 = 0$ 的两根，则该直角三角形的面积是（）

A、6 B、12 C、12或 $\frac{3 \sqrt{7}}{2}$ D、6或 $\frac{3 \sqrt{7}}{2}$

查看试题解析
6. 若关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 4 m - 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $(x_{1} + 2) (x_{2} + 2) - 2 x_{1} x_{2} = 17$ ，则 $m =$ （）

A、2或6 B、2或8 C、2 D、6

查看试题解析
7. 若 $x_{1} ， x_{2}$ 是方程 $x^{2} - 2 x - 3 = 0$ 的两个实数根，则 $x_{1} \cdot x_{2}^{2}$ 的值为（）

A、3或-9 B、-3或9 C、3或-6 D、-3或6

查看试题解析
8. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - a = 0$ 的两根分别记为 $x_{1}$ ， $x_{2}$ ，若 $x_{1} = - 1$ ，则 $a - x_{1}^{2} - x_{2}^{2}$ 的值为（）

A、7 B、-7 C、6 D、-6

查看试题解析
9. 等腰三角形的一边长是3，另两边的长是关于 $x$ 的方程 $x^{2} - 4 x + k = 0$ 的两个根，则 $k$ 的值为（）

A、3 B、4 C、3或4 D、7

查看试题解析
10. 某校八年级组织一次篮球赛，各班均组队参赛，赛制为单循环形式（每两班之间都赛一场），共需安排15场比赛，则八年级班级的个数为（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题（每题3分，共18分）

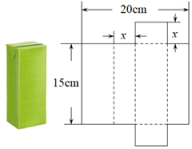
11. 若关于x的方程（m+2）x^|m|＋2x-3＝0是一元二次方程，则m＝.

查看试题解析
12. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
13. 一元二次方程 $x^{2} - 4 x + 3 = 0$ 配方为 ${(x - 2)}^{2} = k$ ，则k的值是.

查看试题解析
14. 已知 $m ， n$ 是一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两个根，则 $\frac{1}{m} + \frac{1}{n} =$ ．

查看试题解析
15. 设 $x_{1}$ 与 $x_{2}$ 为一元二次方程 $\frac{1}{2} x^{2} + 3 x + 2 = 0$ 的两根，则 ${(x_{1} - x_{2})}^{2}$ 的值为．

查看试题解析
16. 你知道吗，对于一元二次方程，我国古代数学家还研究过其几何解法呢！以方程 $x^{2} + 5 x - 14 = 0$ 即 $x (x + 5) = 14$ 为例加以说明.数学家赵爽（公元3～4世纪）在其所著的《勾股圆方图注》中记载的方法是：构造图（如下面左图）中大正方形的面积是 ${(x + x + 5)}^{2}$ ，其中它又等于四个矩形的面积加上中间小正方形的面积，即 $4 \times 14 + 5^{2}$ ，据此易得 $x = 2$ .那么在下面右边三个构图（矩形的顶点均落在边长为1的小正方形网格格点上）中，能够说明方程 $x^{2} - 4 x - 12 = 0$ 的正确构图是.（只填序号）

查看试题解析

三、解答题（共8题，共72分）

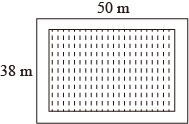
17. 解方程：

(1)、3x²-5x+1=0（配方法）；

(2)、(x+3)(x-1)=5（公式法）．

查看试题解析
18. 如图，在长为50 m，宽为38 m的矩形地面内的四周修筑同样宽的道路，余下的铺上草坪.要使草坪的面积为1260 m² ，道路的宽应为多少？

查看试题解析
19. 列方程（组）解应用题
端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：

小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克．

根据他们的对话，解决下面所给问题：超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？

查看试题解析
20. 若x₁ ， x₂是关于x的一元二次方程ax²+bx+c＝0的两个根，则x₁+x₂＝﹣ $\frac{b}{a}$ ，x₁•x₂＝ $\frac{c}{a}$ .现已知一元二次方程px²+2x+q＝0的两根分别为m，n.

(1)、若m＝2，n＝﹣4，求p，q的值；

(2)、若p＝3，q＝﹣1，求m+mn+n的值.

查看试题解析
21. 直播购物逐渐走进了人们的生活．某电商在抖音上对一款成本价为40元的小商品进行直播销售，如果按每件60元销售，每天可卖出20件．通过市场调查发现，每件小商品售价每降低5元，日销售量增加10件．

(1)、若日利润保持不变，商家想尽快销售完该款商品，每件售价应定为多少元？

(2)、小明的线下实体商店也销售同款小商品，标价为每件62.5元．为提高市场竞争力，促进线下销售，小明决定对该商品实行打折销售，使其销售价格不超过（1）中的售价，则该商品至少需打几折销售？

查看试题解析
22. 对于三个数 $a$ 、 $b$ 、 $c$ ，用 $M {a ， b ， c}$ 表示这三个数的中位数，用 $\max {\dot{a} ， b ， c}$ 表示这三个数中最大数，例如： $M {- 2 ， - 1 ， 0} = - 1$ ， $\max {- 2 ， - 1 ， 0} = 0$ ， $\max {- 2 ， - 1 ， a} = {\begin{matrix} a (a \geq - 1) \\ - 1 (a < - 1) \end{matrix}$ .
解决问题：

(1)、填空： $M {\sin 45 ° ， \cos 60 ° ， \tan 60 °} =$ ，如果 $\max {3 ， 5 - 3 x ， 2 x - 6} = 3$ ，则 $x$ 的取值范围为；

(2)、如果 $2 \cdot M {2 ， x + 2 ， x + 4} = \max {2 ， x + 2 ， x + 4}$ ，求 $x$ 的值；

(3)、如果 $M {9 ， x^{2} ， 3 x - 2} = \max {9 ， x^{2} ， 3 x - 2}$ ，求 $x$ 的值.

查看试题解析
23. 阅读材料：
材料1：若一元二次方程ax²+bx+c＝0（a≠0）的两个根为x₁ ， x₂则x₁+x₂ $= - \frac{b}{a}$ ， x_1*x₂ $= \frac{c}{a}$ ．

材料2 ：已知实数m，n满足m²﹣m﹣1＝0，n²﹣n﹣1＝0，且m≠n，求 $\frac{n}{m} + \frac{m}{n}$ 的值．

解：由题知m，n是方程x²﹣x﹣1＝0的两个不相等的实数根，根据材料1得m+n＝1，mn＝﹣1，

所以 $\frac{n}{m} + \frac{m}{n} = \frac{n^{2} + m^{2}}{m n} = \frac{(m + n)^{2} - 2 m n}{m n} = \frac{1 - 2 \times (- 1)}{- 1} = - 3$ ．

根据上述材料解决以下问题：

(1)、材料理解：
一元二次方程5x²+10x﹣1＝0的两个根为x₁ ， x₂ ，则x₁+x₂＝， x₁x₂＝．

(2)、类比探究：
已知实数m，n满足7m²﹣7m﹣1＝0，7n²﹣7n﹣1＝0，且m≠n，求m²n+mn²的值：

查看试题解析
24. 阅读理解：
材料一：若一元二次方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ）的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ .
材料二：已知实数 $m$ ， $n$ 满足 $m^{2} - m - 1 = 0$ ， $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，求 $\frac{n}{m} + \frac{m}{n}$ 的值.
解：由题知 $m$ ， $n$ 是方程 $x^{2} - x - 1 = 0$ 的两个不相等的实数根，根据材料一得 $m + n = 1$ ， $m n = - 1$ ，
∴ $\frac{n}{m} + \frac{m}{n} = \frac{m^{2} + n^{2}}{m n} = \frac{{(m + n)}^{2} - 2 m n}{m n} = \frac{1 + 2}{- 1} = - 3$ .
解决问题：

(1)、已知实数 $s$ ， $t$ 满足 $2 s^{2} - 2 s - 1 = 0$ ， $2 t^{2} - 2 t - 1 = 0$ ，且 $s \neq t$ ，求 $s^{2} t + s t^{2}$ 的值；

(2)、已知实数 $p$ ， $q$ 满足 $p^{2} = 3 p + 2$ ， $2 q^{2} = 3 q + 1$ ，且 $p \neq 2 q$ ，求 $p^{2} + 4 q^{2}$ 的值.

查看试题解析

x	﹣3	﹣2	﹣1	…	4	5	6
x²﹣3x﹣5	13	5	﹣1	…	﹣1	5	13

2022年秋季北师版数学九年级上册第二章 《一元二次方程》单元检测B

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

2022年秋季北师版数学九年级上册第二章《一元二次方程》单元检测B