浙江省湖州市长兴县部分校2022-2023学年九年级上学期返校联考数学试题

试卷更新日期：2022-09-30 类型：开学考试

进入出卷网下载

一、选择题(本题有10小题,每小题3分,共30分)

1. 下列二次根式中，可与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{3}$ B、 $\sqrt{4}$ C、 $\sqrt{6}$ D、 $\sqrt{8}$

查看试题解析
2. 下列由箭头组成的图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 把一元二次方程 $2 (x + 1) + {(2 x - 1)}^{2} = 0$ 化成一般形式，结果正确的是（）

A、 $4 x^{2} - 4 x + 1 = 0$ B、 $4 x^{2} - 2 x + 3 = 0$ C、 $2 x^{2} - 2 x + 3 = 0$ D、 $4 x^{2} + 3 = 0$

查看试题解析
4. 若二次根式 $\sqrt{x^{2}}$ 的值为3，则 $x$ 的值是（）

A、 $\sqrt{3}$ B、3 C、 $\pm 3$ D、9

查看试题解析
5. 小娅在对数据 $26 ， 30 ， 30 ， 43 ， 5 * ， 57$ 进行统计分析时，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果不受影响的统计量是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
6. 一个长方形牧场的面积为8100平方米，长比宽多19米，设宽为x米，由题意可列出的方程是（）

A、 $(x + 19) x = 8100$ B、 $(x - 19) x = 8100$ C、 $(2 x - 19) x = 8100$ D、 $(2 x + 19) x = 8100$

查看试题解析
7. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $P$ ，且当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大，则点 $P$ 的坐标可以是（）

A、 $(2 ， 2)$ B、 $(- 1 ， - 3)$ C、 $(- 5 ， 3)$ D、 $(5 ， 1)$

查看试题解析
8. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤，然后剪出图⑤中的阴影部分，则阴影部分展开铺平后的图形是（）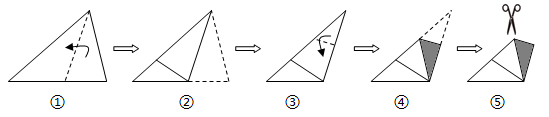

A、等腰三角形 B、直角三角形 C、矩形 D、菱形

查看试题解析
9. 如图，在平面直角坐标系 $x O y$ 中， $M ， N$ 是 $x$ 轴正半轴上两个点，且 $O N = 3 O M$ ，过点 $M$ 作 $x$ 轴的垂线，分别与反比例函数 $y = \frac{3}{x}$ 和 $y = - \frac{2}{x}$ 的图象交于 $A ， B$ 两点，过点 $N$ 作 $x$ 轴的垂线，分别与反比例函数 $y = \frac{3}{x}$ 和 $y = - \frac{2}{x}$ 的图象交于 $C ， D$ 两点，则四边形ABCD的面积是（）

A、 $\frac{20}{3}$ B、10 C、 $\frac{15}{2}$ D、随点 $M$ 位置的变化而变化

查看试题解析
10. 如图，以菱形 $A B C D$ 的边 $A D$ 为对角线，作正方形 $A E D F$ ，点 $E$ 恰好落在 $C B$ 的延长线上，则 $∠ B A E$ 的度数是（）

A、 $1 0^{∘}$ B、 $1 5^{∘}$ C、 $2 0^{∘}$ D、 $2 5^{∘}$

查看试题解析

二、填空题(本题有6小题,每小题4分,共24分)

11. 已知一组数据的方差为4，这组数据的标准差是.

查看试题解析
12. 用配方法解方程 $x^{2} + 4 x - 3 = 0$ ，配方得 ${(x + m)}^{2} = 7$ ，常数 $m$ 的值是.

查看试题解析
13. 如果一个八边形的每一个内角都相等，那么它的一个内角的度数为.

查看试题解析
14. 如果一个三角形的三边长分别为 $a ， b ， c$ ，记 $p = \frac{a + b + c}{2}$ ，那么这个三角形的面积 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ，这就是著名的海伦一秦九韶公式.若一个三角形的三边长分别为 $4 ， 5 ， 6$ ，则这个三角形的面积为.

查看试题解析
15. 如图，在 $▱ A B C D$ 中，对角线 $A C ， B D$ 交于点 $O$ ，若 $B D ⊥ A B$ ，且 $A C = 10 ， A B = 4$ ，则 $B D$ 的长是.

查看试题解析
16. 如图，四边形 $O A B C$ 为矩形，点 $A$ 在第三象限，点 $A$ 关于 $O B$ 的对称点为点 $D$ ，点 $B$ ， $D$ 都在函数 $y = - \frac{3 \sqrt{2}}{x} (x < 0)$ 的图象上， $B E ⊥ y$ 轴于点 $E$ .若 $D C$ 的延长线交 $y$ 轴于点 $F$ ，当矩形 $O A B C$ 的面积为6时， $\frac{O F}{O E}$ 的值为.

查看试题解析

三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)

17. 计算： $(\sqrt{12} - 3) \div \sqrt{3}$ .

查看试题解析
18. 已知关于 $x$ 的方程 $2 x^{2} + 2 k x + k - 1 = 0$ ，

(1)、求证：无论 $k$ 为何值，方程总有两个不相等实数根；

(2)、若 $x = - 1$ 是该方程的一个根，求方程的另一个根.

查看试题解析
19. 已知 $△ A B C$ 中， $A B = 1 ， B C = 2 \sqrt{2} ， A C = \sqrt{5}$ .

(1)、在 $4 \times 4$ 的网格中画出 $△ A B C$ ，使它的顶点都在方格的顶点上(每个小方格的边长为1 $)$ ；

(2)、在(1)中的网格里找一点 $D$ (在方格的顶点上)，使得 $△ A B C$ 的面积与 $△ B C D$ 的面积相等.

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $E ， F$ 分别为 $A B ， C D$ 边上的中点， $A C$ 是对角线.

(1)、求证： $A F / / C E$ ；

(2)、若 $A C ⊥ B C ， A B = 4$ ，求四边形 $A E C F$ 的周长.

查看试题解析

21. 某中学组织七、人年级全体学生开展了“禁毒知识”网上竞赛活动，为了解竞赛情况，从七、八年级中各随机抽取了10名同学的成绩(满分为100分).

收集数据：

七年级	90	95	95	80	90	80	85	100	85	100
八年级	85	85	95	80	95	90	90	90	100	90

整理数据：

	80	85	90	95	100
七年级	2	2	2	2	2
八年级	1	2	4	2	1

分析数据：

年级	平均数	中位数	众数	方差
七年级	90	____	90	50
八年级	____	90	90	30

根据以上信息回答下列问题：

(1)、请完成表格中的空格.

(2)、通过数据分析，你认为哪个年级学生的成绩比较好?请说明理由.

(3)、若该校七、人年级共有1600人，本次竞赛成绩不低于95分的为“优秀”，试估计这两个年级共有多少名学生达到“优秀”.

查看试题解析

22. 某商店经市场调查发现：某种商品的周销售量 $y$ (件)与售价 $x$ (元/件)的关系为 $y = - 2 x + 200$ ，其售价与周销售利润 $w$ (元)的三组对应值如下表：

售价x(元/件)

50

55

70

周销售利润w(元)

1000

1350

1800

注：周销售利润=周销售量 $\times ($ 售价一进价)

(1)、求该商品的进价；

(2)、求当该商品的售价是多少元/件时，周销售利润为1600元?

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，已知点 $A (- 3 \sqrt{3} ， 3)$ ，点 $B (- 6 ， 0)$ .

(1)、若将 $△ O A B$ 沿 $x$ 轴向右平移 $m$ 个单位，此时点 $A$ 恰好落在反比例函数 $y = \frac{6 \sqrt{3}}{x}$ 的图象上，求 $m$ 的值；

(2)、若 $△ O A B$ 绕点 $O$ 按逆时针方向旋转 $α$ 度 $(0 < α < 180)$ .
①当 $α = 3 0^{∘}$ 时，点 $B$ 恰好落在反比例函数 $y = \frac{k}{x}$ 图象上，求 $k$ 的值；

②问点 $A ， B$ 能否同时落在(1)中的反比例函数的图象上?若能，直接写出 $α$ 的值；若不能，请说明理由.

查看试题解析
24. 如图，在矩形 $A B C D$ 中， $A B = 8 ， B C = 4 ， O$ 是对角线 $B D$ 中点.过 $O$ 点的直线与矩形的一组对边 $A B ， C D$ 分别相交于点 $F$ 和点 $E . B^{'}$ 与 $B$ 关于直线 $E F$ 对称，连结 $B E$ ， $D B^{'} ， E B^{'} ， O B^{'}$ .

(1)、求证： $O E = O F$ ；

(2)、判断 $D B^{'}$ 与 $O E$ 的位置关系，并说明理由；

(3)、若四边形 $O E B^{'} D$ 是平行四边形，求线段 $E F$ 长.

查看试题解析

售价x(元/件)	50	55	70
周销售利润w(元)	1000	1350	1800