浙江省杭州十三中2022-2023学年九年级上学期开学考试数学试卷

试卷更新日期：2022-09-30 类型：开学考试

进入出卷网下载

一、选择题（每小题3分，共30分）.

1. $- \sqrt{2} \times \sqrt{5}$ ＝（）

A、 $\sqrt{10}$ B、- $\sqrt{10}$ C、 $\sqrt{7}$ D、- $\sqrt{7}$

查看试题解析
2. 如图，矩形纸片ABCD中，AB＝6cm，BC＝8cm，现将其沿AE对折，使得点B落在边AD上的点B₁处，折痕与边BC交于点E，则CE的长为（）

A、2cm B、3cm C、4cm D、6cm

查看试题解析
3. 某校六一活动中，10位评委给某个节目的评分各不相同，去掉1个最高分和1个最低分，剩下的8个评分与原始的10个评分相比（）

A、平均数一定不发生变化 B、中位数一定不发生变化 C、方差一定不发生变化 D、众数一定不发生变化

查看试题解析
4. 将抛物线y＝3x²的图象先向右平移2个单位，再向上平移5个单位后，得到的抛物线解析式是（）

A、y＝3（x﹣2）²﹣5 B、y＝3（x﹣2）²+5 C、y＝3（x+2）²﹣5 D、y＝3（x+2）²+5

查看试题解析
5. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有30个，黑球有n个．随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则n的值约为（）

A、20 B、30 C、40 D、50

查看试题解析
6. 若关于 $x$ 的一元二次方程 $x^{2} + 2 x + m = 0$ 有两个不相等的实数根，则 $m$ 的值可能是（）

A、0 B、1 C、2 D、3

查看试题解析
7. 如图，▱ABCD的对角线AC，BD交于点O，E是AD的中点，连结OE，AC＝8，BC＝10，若AC⊥CD，则OE等于（）

A、3 B、4 C、5 D、6

查看试题解析
8. 已知点A（1，y₁），B（2，y₂），C（﹣2，y₃）都在反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象上，则（）

A、y₁＞y₂＞y₃ B、y₃＞y₂＞y₁ C、y₂＞y₃＞y₁ D、y₁＞y₃＞y₂

查看试题解析
9. 如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于H，连接OH，∠DHO＝α，则∠DAB的度数是（）

A、α B、2α C、90°﹣α D、90°﹣2α

查看试题解析
10. 二次函数y＝ax²+bx+1（a≠0）的图象的顶点在第一象限，且过点（﹣1，0），设t＝a+b+1，则t的取值范围为（）

A、0＜t＜2 B、﹣1＜t＜0 C、t＜﹣1 D、t＜2

查看试题解析

二、填空题（每小题4分，共24分）

11. 投掷一枚均匀的骰子，偶数朝上的概率是.

查看试题解析
12. 如图，在矩形ABCD中，E，F分别是AD，AB的中点，若AC＝4，则EF的长是.

查看试题解析
13. 如图抛物线y＝ax²+bx+c的对称轴是直线x＝﹣1，与x轴的一个交点为（﹣5，0），则不等式ax²+bx+c＞0的解集为.

查看试题解析
14. 已知四个二次函数的图象如图所示，那么a₁ ， a₂ ， a₃ ， a₄的大小关系是．（请用“＞”连接排序）

查看试题解析
15. 对于反比例函数y＝ $\frac{6}{x}$ ，当x＞2时，y的取值范围是.

查看试题解析
16. 如图是一张矩形纸片ABCD，点E在AC边上，把△DCE沿直线DE折叠，使点C落在对角线BD上的点F处；点G在AB边上，把△DAG沿直线DG折叠，使点A落在线段DF上的点H处．若HF＝1，BF＝8，则BD＝，矩形ABCD的面积＝．

查看试题解析

三、解答题（共66分）

17.

(1)、计算： $\frac{1}{2} \sqrt{24} - 2 \sqrt{2} \times \sqrt{3}$ .

(2)、解方程：x²﹣4x﹣1＝0.

查看试题解析
18. 在探究欧姆定律时，小明发现小灯泡电路上的电压保持不变，通过小灯泡的电流越大，灯就越亮.设选用小灯泡的电阻为R（Ω），通过的电流强度为I（A）.（欧姆定律公式： $I = \frac{U}{R}$ ）

(1)、若电阻为40Ω，通过的电流强度为0.30A，求I关于R的函数表达式；

(2)、如果电阻小于40Ω，那么与原来的相比，小灯泡的亮度将发生什么变化？并说明理由.

查看试题解析
19. 一个不透明的布袋中装有3个只有颜色不同的球，其中1个黄球、2个红球.

(1)、任意摸出1个球，记下颜色后不放回，再任意摸出1个球，求两次摸出的球恰好都是红球的概率（要求画树状图或列表）；

(2)、现再将n个黄球放入布袋，搅匀后，使任意摸出1个球是黄球的概率为 $\frac{3}{4}$ ，求n的值.

查看试题解析
20. 已知，如图，在菱形ABCD中，AC为对角线，E是AC上的点，分别连结BE，DE并延长交CD于点G，交BC于点F.

(1)、求证：BE＝DE；

(2)、若DG⊥BF，∠BAD＝60°，AB＝2，求CE的长.

查看试题解析
21. 十三中为了创建城市文明单位，准备在操场的墙（线段MN所示，不考虑墙体长度）外开辟一处长方形的土地进行绿化美化，除墙体外三面要用栅栏围起来，计划用栅栏40米（正好用完）.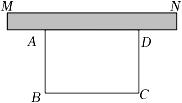

(1)、长方形的各边的长为多少米时，长方形的面积最大？

(2)、若9≤AB≤12，试求长方形面积S的取值范围.

查看试题解析
22. 已知二次函数y＝mx²﹣2mx+3，其中m≠0.

(1)、若二次函数的图象经过（1，4），求二次函数表达式；

(2)、若该二次函数图象开口向上，当﹣1≤x≤2时，二次函数图象的最高点为M，最低点为N，点M的纵坐标为6，求点M和点N的坐标；

(3)、在二次函数图象上任取两点（x₁ ， y₁），（x₂ ， y₂），当a≤x₁＜x₂≤a+2时，总有y₁＞y₂ ，求a的取值范围.

查看试题解析
23. 如图①，已知正方形ABCD中，E，F分别是边AD，CD上的点（点E，F不与端点重合），且AE＝DF，BE，AF交于点P，过点C作CH⊥BE交BE于点H.

(1)、求证：AF⊥BE；

(2)、若AB＝2 $\sqrt{3}$ ， AE＝2，试求线段PH的长；

(3)、如图②，连接CP并延长交AD于点Q，若点H是BP的中点，试求 $\frac{C P}{P Q}$ 的值.

查看试题解析