陕西省咸阳市兴平市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-30 类型:期中考试
一、单选题
-
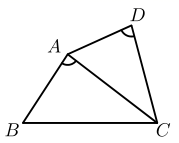
1. 若线段 , , , 是成比例线段,且 , , ,则 ( )A、 B、 C、 D、2. 把方程 化成一元二次方程的一般形式,则二次项系数、一次项系数、常数项分别是( )A、 B、 C、 D、3. 在相同条件下,移植10000棵幼苗,有8000棵幼苗成活,估计在相同条件下移植一棵这种幼苗成活的概率为( )A、0.1 B、0.2 C、0.9 D、0.84. 如图,在四边形 中,如果 ,那么下列条件中不能判定 和 相似的是( )
 A、 B、 是 的平分线 C、 D、5. 若关于的一元二次方程没有实数根,则的取值范围是( )A、 B、 C、 D、6. 如图,点P是正方形ABCD的对角线BD上的一点,且BP=BC,则∠PCD的度数是( )
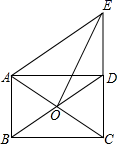
A、 B、 是 的平分线 C、 D、5. 若关于的一元二次方程没有实数根,则的取值范围是( )A、 B、 C、 D、6. 如图,点P是正方形ABCD的对角线BD上的一点,且BP=BC,则∠PCD的度数是( )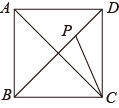 A、22.5° B、45° C、60° D、67.5°7. 一天晚上,小伟帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小伟只好把杯盖和茶杯随机搭配在一起,则颜色搭配正确的概率是( )A、 B、 C、 D、8. 如图,在正方形中,点、分别在、的延长线上,且 , 连接 , 交于点 , 并分别与边 , 交于点 , , 连接 , 下列结论:①;②;③S四边形OECF,其中正确结论的个数是( )
A、22.5° B、45° C、60° D、67.5°7. 一天晚上,小伟帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小伟只好把杯盖和茶杯随机搭配在一起,则颜色搭配正确的概率是( )A、 B、 C、 D、8. 如图,在正方形中,点、分别在、的延长线上,且 , 连接 , 交于点 , 并分别与边 , 交于点 , , 连接 , 下列结论:①;②;③S四边形OECF,其中正确结论的个数是( )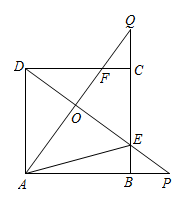 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
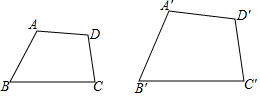
9. 方程的根为 .10. 如图,四边形四边形 , 若 , , , 则的度数为 .
 11. 如果菱形的一条对角线长是另一条长的 倍,这个菱形的面积等6 ,那么这个菱形的周长等于 .12. 某校去年对学生所用实验器材的投资是10万元,预计今明两年的投资总额为26.4万元,求今明两年该校在实验器材投资上的年平均增长率,设今明两年该校在实验器材投资上的年平均增长率为 , 则可列方程为 .13. 如图,正方形ABCD中,点E为AB的中点,M、N分别为AD、BC上的点,若 , , , 则MN的长为 .
11. 如果菱形的一条对角线长是另一条长的 倍,这个菱形的面积等6 ,那么这个菱形的周长等于 .12. 某校去年对学生所用实验器材的投资是10万元,预计今明两年的投资总额为26.4万元,求今明两年该校在实验器材投资上的年平均增长率,设今明两年该校在实验器材投资上的年平均增长率为 , 则可列方程为 .13. 如图,正方形ABCD中,点E为AB的中点,M、N分别为AD、BC上的点,若 , , , 则MN的长为 .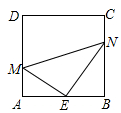
三、解答题
-
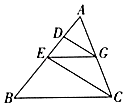
14. 解方程:15. 已知:k是方程3x2﹣2x﹣1=0的一个根,求代数式9k2﹣6k+7的值.16. 如图,在中,点在上,过作交于点 , 连接 , 过点作 交于 . 求证: .
 17. 在一个不透明的袋中装有材质、大小完全相同的红球和黑球共100个,小明每次摇匀后随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,估计袋中红球的个数.18. 已知关于的一元二次方程有两个实数根,求的取值范围.19. 如图,在中,点 , 分别在线段 , 上,连接 , , , , 求证:四边形是菱形.
17. 在一个不透明的袋中装有材质、大小完全相同的红球和黑球共100个,小明每次摇匀后随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,估计袋中红球的个数.18. 已知关于的一元二次方程有两个实数根,求的取值范围.19. 如图,在中,点 , 分别在线段 , 上,连接 , , , , 求证:四边形是菱形.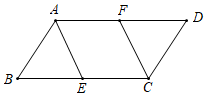 20. 如图,在和中,、分别是、上一点, , 当 , 时,求证: .
20. 如图,在和中,、分别是、上一点, , 当 , 时,求证: .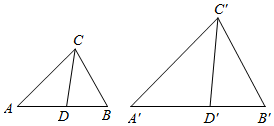 21. 已知,如图,在 中, 是两锐角平分线的交点, , ,垂足分别为 , ,求证:四边形 是正方形.
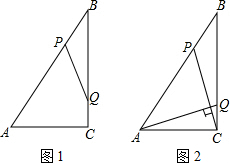
21. 已知,如图,在 中, 是两锐角平分线的交点, , ,垂足分别为 , ,求证:四边形 是正方形.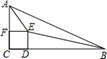 22. 如图,在锐角中,点 , 分别在边 , 上,连接 , 于点 , 于点 , .
22. 如图,在锐角中,点 , 分别在边 , 上,连接 , 于点 , 于点 , .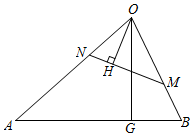 (1)、求证:;(2)、若 , , 求的值.23. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
(1)、求证:;(2)、若 , , 求的值.23. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.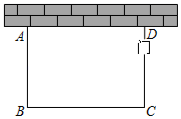 24. 辽宁省某城市力争创建精神文明城市,需要全民一心,大家共同打造自己美好的家园.小明的爸爸和妈妈申请利用业余时间到社区义务服务,根据社区的安排,小明的爸爸和妈妈被随机分配到A、B、C、D四个共享单车停车点中的一个地点服务.(1)、小明的爸爸会被分到A停车点服务的概率是;(2)、小明的爸爸和妈妈分配在同一停车点的概率是多少?(请用画树状图或列表的方法列出所有可能结果)
24. 辽宁省某城市力争创建精神文明城市,需要全民一心,大家共同打造自己美好的家园.小明的爸爸和妈妈申请利用业余时间到社区义务服务,根据社区的安排,小明的爸爸和妈妈被随机分配到A、B、C、D四个共享单车停车点中的一个地点服务.(1)、小明的爸爸会被分到A停车点服务的概率是;(2)、小明的爸爸和妈妈分配在同一停车点的概率是多少?(请用画树状图或列表的方法列出所有可能结果)