陕西省咸阳市武功县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-30 类型:期中考试
一、单选题
-
1. 如图,直线 , 直线、与、、分别交于点、、和点、、 , 若 , , 则的长是( )
 A、4 B、7 C、6 D、122. 菱形和矩形都具有的性质是( )A、对角线互相平分 B、有一组邻边相等 C、对角线相等 D、对角线互相垂直3. 若关于x的一元二次方程x2+3x﹣k=0有两个不相等的实数根,则实数k的取值范围为( )A、k>﹣ B、k≥﹣ C、k<﹣ D、k≤﹣4. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、一组对边平行且对角线相等的四边形是矩形 D、四条边都相等的四边形是菱形5. 在一个不透明的盒子中装有m个除颜色外完全相同的球,这m个球中只有4个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则m的值大约为( )A、10 B、12 C、16 D、206. 如图,在矩形 中,对角线 与 相交于点 ,过点 作 ,垂足为点 ,若 ,则 ( )
A、4 B、7 C、6 D、122. 菱形和矩形都具有的性质是( )A、对角线互相平分 B、有一组邻边相等 C、对角线相等 D、对角线互相垂直3. 若关于x的一元二次方程x2+3x﹣k=0有两个不相等的实数根,则实数k的取值范围为( )A、k>﹣ B、k≥﹣ C、k<﹣ D、k≤﹣4. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、一组对边平行且对角线相等的四边形是矩形 D、四条边都相等的四边形是菱形5. 在一个不透明的盒子中装有m个除颜色外完全相同的球,这m个球中只有4个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则m的值大约为( )A、10 B、12 C、16 D、206. 如图,在矩形 中,对角线 与 相交于点 ,过点 作 ,垂足为点 ,若 ,则 ( ) A、 B、 C、 D、7. 如图,是菱形的对角线 , 的交点, , 分别是 , 的中点.下列结论中正确的是( )
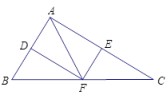
A、 B、 C、 D、7. 如图,是菱形的对角线 , 的交点, , 分别是 , 的中点.下列结论中正确的是( )①;②四边形是菱形;③四边形的面积为 , ④ .
 A、①② B、②④ C、②③ D、③④
A、①② B、②④ C、②③ D、③④二、多选题
-
8. 如图,在△ABC中,点P为AB上一点,给出下列四个条件中能满足△APC和△ACB相似的条件是( )
 A、∠ACP=∠B B、∠APC=∠ACB C、AC2=AP·AB D、AB·CP=AP·CB
A、∠ACP=∠B B、∠APC=∠ACB C、AC2=AP·AB D、AB·CP=AP·CB三、填空题
-
9. 已知一元二次方程2x2+mx﹣4=0的一个根是 ,则该方程的另一个根是 .10. 如果关于 的一元二次方程 的一个解是 ,那么代数式 的值是 .11. 若 , 则= .12. 参加足球联赛的每两队之间都进行两场比赛,共要比赛210场,则参加比赛的足球队共有个.13. 如图,正方形的边长为 , 为边的中点,点在边上移动,点关于直线的对称点记为 , 连接、、 . 当四边形为正方形时,的长为 .

四、解答题
-
14. 用适当的方法解方程: .15. 如图,已知 , 、相交于点 , 若 , , .
 (1)、求证:;(2)、求线段的长.16. 如图,已知 , , , , , 求证: .
(1)、求证:;(2)、求线段的长.16. 如图,已知 , , , , , 求证: . 17. 如图,已知四边形ABCD是平行四边形,点E,F分别是BC,CD上的点,∠AEB=∠AFD,BE=DF.求证:四边形ABCD是菱形.
17. 如图,已知四边形ABCD是平行四边形,点E,F分别是BC,CD上的点,∠AEB=∠AFD,BE=DF.求证:四边形ABCD是菱形. 18. 袁隆平是我国研究与发展杂交水稻的开创者,被誉为“杂交水稻之父”,成功选育了世界上第一个实用高产杂交水稻品种.某农业基地现有杂交水稻种植面积20公顷,计划两年后将杂交水稻种植面积增至24.2公顷,求该农业基地杂交水稻种植面积的年平均增长率.19. 有一块长12cm,宽8cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为32cm2的无盖的盒子,求截去的小正方形的边长.
18. 袁隆平是我国研究与发展杂交水稻的开创者,被誉为“杂交水稻之父”,成功选育了世界上第一个实用高产杂交水稻品种.某农业基地现有杂交水稻种植面积20公顷,计划两年后将杂交水稻种植面积增至24.2公顷,求该农业基地杂交水稻种植面积的年平均增长率.19. 有一块长12cm,宽8cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为32cm2的无盖的盒子,求截去的小正方形的边长. 20. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
20. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB. (1)、求∠ABC的度数.(2)、如果AC=6 , 求DE的长.21. 九年级某班要召开一次“走进祖国英雄,讲好中国故事”主题班会活动,张老师制作了编号为A、B、C、D的4张卡片(如图,除了编号和内容外,其余完全相同),将它们背面朝上洗匀后放在桌面上.
(1)、求∠ABC的度数.(2)、如果AC=6 , 求DE的长.21. 九年级某班要召开一次“走进祖国英雄,讲好中国故事”主题班会活动,张老师制作了编号为A、B、C、D的4张卡片(如图,除了编号和内容外,其余完全相同),将它们背面朝上洗匀后放在桌面上. (1)、小东随机抽取1张卡片,则抽到卡片编号为B的概率为;(2)、小东从4张卡片中随机抽取一张(不放回),小海再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述相应英雄故事,求小东、小海两人中恰好有一人讲述“卫国边英雄”陈红军故事的概率(请用“画树状图”或“列表”等方法写出过程)22. 交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门绘制出2021年五一小长假期间旅游情况统计图,根据以下信息解答下列问题:
(1)、小东随机抽取1张卡片,则抽到卡片编号为B的概率为;(2)、小东从4张卡片中随机抽取一张(不放回),小海再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述相应英雄故事,求小东、小海两人中恰好有一人讲述“卫国边英雄”陈红军故事的概率(请用“画树状图”或“列表”等方法写出过程)22. 交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门绘制出2021年五一小长假期间旅游情况统计图,根据以下信息解答下列问题: (1)、五一小长假期间,该市旅游景区景点共接待游客 ▲ 万人,请补全条形统计图.(2)、根据2021年到该市旅游人数的情况,预计2022年五一小长假期间将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中任选一个景点旅游,求两个旅行团同时选择去同一景点的概率是多少?23. 数学小组想利用所学知识测量一棵树的高度 . 在第一次测量中,小莉来回走动,走到点D时,其影子末端与树梢影子末端重合于点H,测得米.随后,组员在直线上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应位置为点G.镜子不动,小莉从点D沿着直线后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时米.如图,已知 , , , 小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度 .
(1)、五一小长假期间,该市旅游景区景点共接待游客 ▲ 万人,请补全条形统计图.(2)、根据2021年到该市旅游人数的情况,预计2022年五一小长假期间将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中任选一个景点旅游,求两个旅行团同时选择去同一景点的概率是多少?23. 数学小组想利用所学知识测量一棵树的高度 . 在第一次测量中,小莉来回走动,走到点D时,其影子末端与树梢影子末端重合于点H,测得米.随后,组员在直线上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应位置为点G.镜子不动,小莉从点D沿着直线后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时米.如图,已知 , , , 小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度 . 24. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若销售单价降低5元,那么平均每天销售数量为多少件?(2)、若该商店每天销售利润为1200元,问每件商品可降价多少元?
24. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若销售单价降低5元,那么平均每天销售数量为多少件?(2)、若该商店每天销售利润为1200元,问每件商品可降价多少元?
-