陕西省西安市莲湖区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、x²＝0 B、3x＋2y＝7 C、x²﹣2x＋1＞0 D、 $\frac{1}{x}$ ＝x＋2

查看试题解析
2. 已知方程3x²﹣（k﹣1）x﹣k＋7＝0的一个根为0，则k的值为（）

A、3 B、﹣3 C、7 D、﹣7

查看试题解析
3. 矩形、菱形、正方形都具有的性质是（　　）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分对角

查看试题解析
4. 为绿化、美化环境，某园林部门计划在某地修建一个面积为100平方米的矩形花园，它的长比宽多10米，设宽为x米，可列方程为（）

A、x（x﹣10）＝100 B、x（x＋10）＝100 C、2x＋2（x＋10）＝100 D、2x＋2（x﹣10）＝100

查看试题解析
5. 某小组做“当试验次数很大时，用频率估计概率”的试验时，统计了某一结果出现的频率．表格如下，则符合这一结果的试验最有可能的是（）
次数
100
200
300
400
500
600
700
800
900
1000
频率
0.60
0.30
0.50
0.36
0.42
0.38
0.41
0.39
0.40
0.40

A、掷一枚质地均匀的骰子，向上面的点数是“5” B、掷一枚一元的硬币，正面朝上 C、不透明的袋子里有2个红球和3个黄球，除颜色外都相同，从中任取一球是红球 D、三张扑克牌，分别是3、5、5，背面朝上洗匀后，随机抽出一张是5

查看试题解析
6. 一元二次方程 $x^{2} - 6 x - 1 = 0$ 配方后可变形为（）

A、 ${(x - 3)}^{2} = 8$ B、 ${(x + 3)}^{2} = 8$ C、 ${(x + 3)}^{2} = 10$ D、 ${(x - 3)}^{2} = 10$

查看试题解析
7. 将分别标有“中”“国”“加”“油”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀随机摸出一球，不放回；再随机摸出一球．两次摸出的球上的汉字能组成“加油”的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，点P是Rt△ABC中斜边AC (不与A，C重合)上一动点，分别作PM⊥AB于点M，作PN⊥BC于点N，连接BP、MN，若AB=6，BC=8，当点P在斜边AC上运动时，则MN的最小值是（）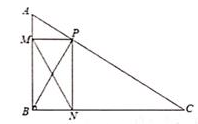

A、1.5 B、2 C、4.8 D、2.4

查看试题解析

二、填空题

9. 在Rt $△ A B C$ 中，∠C＝90°，点D是AB边的中点，若AB＝8，则CD＝．

查看试题解析
10. 小亮与小明一起玩“石头、剪刀、布”的游戏，两同学同时出“剪刀”的概率是．

查看试题解析
11. 已知关于x的一元二次方程x²＋（2m﹣1）x＋m²﹣3＝0有实数根，则实数m的取值范围是．

查看试题解析
12. 如图，在矩形ABCD中，对角线AC与BD相交于点O，∠AOB＝60°，对角线AC所在的直线绕点O顺时针旋转α角度（0°＜α＜120°），所得的直线l分别交AD，BC于点E，F．当旋转角α为时，四边形AFCE为菱形．

查看试题解析
13. 如图，在正方形ABCD中，E是对角线BD上的一点，F是CB延长线上一点，连接CE，EF，AF，AE．若DE＝DC，EF＝EC，则∠AFE的度数为．

查看试题解析

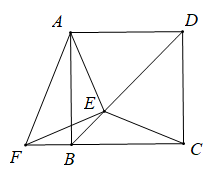
三、解答题

14. 用因式分解法解方程：2（x﹣3）＝3x（x﹣3）．

查看试题解析
15.
如图，正方形ABCD中，点E，F分别在AD，CD上，且AE=DF，连接BE，AF．求证：BE=AF．

查看试题解析
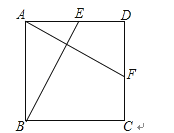16. 电动自动车已成为市民日常出行的首选工具．据某市某品牌电动自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月份销售216辆．求该品牌电动自行车销售量的月均增长率.

查看试题解析
17. 如图，在△ABC中，AB⊥BC，请用尺规作图法，在平面内求作一点D，使四边形ABCD为矩形．（保留作图痕迹，不写作法）

查看试题解析
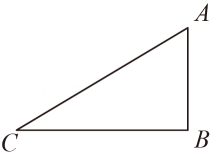18. 桌面上放有不透明的四张卡片，每张卡片正面都写有一个数字，分别是1，2，3，4，它们除数字外其余全部相同，现将它们背面朝上洗均匀.随机抽取一张卡片，记下数字后放回，洗匀后再随机抽取一张卡片，请用列表或画树状图的方法求出两次数字和为4的概率.

查看试题解析
19. 如图，点F在△ABC的边AC上，且AB＝AF，过点F、B分别作AB、AC的平行线相交于点E，连接BF．求证：四边形ABEF是菱形．

查看试题解析
20. 某景区检票口有A、B、C、D共4个检票通道．甲、乙两人到该景区游玩，两人分别从4个检票通道中随机选择一个检票．

(1)、甲选择A检票通道的概率是；

(2)、求甲乙两人选择的检票通道恰好相同的概率．

查看试题解析
21. 如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，问几秒钟时△PBQ的面积等于8cm．

查看试题解析
22. 甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示．游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．

(1)、用列表法（或画树状图）求甲获胜的概率；

(2)、你认为这个游戏规则对双方公平吗？请简要说明理由．

查看试题解析
23. 将一根长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．

(1)、要使这两个正方形的面积之和等于17cm² ，那么这段铁丝剪成两段后的长度分别是多少？

(2)、两个正方形的面积之和可能等于10cm²吗？若能，求出两段铁丝的长度；若不能，请说明理由．

查看试题解析
24. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．

(1)、求证：四边形OEFG是矩形．

(2)、若AD＝12，EF＝4 $\sqrt{2}$ ，求OE和BG的长．

查看试题解析
25. 直播购物逐渐走进了人们的生活．某电商在抖音上对一款成本价为30元的小商品进行直播销售，如果按每件40元销售，每月可卖出600件，通过市场调查发现，每件小商品售价每上涨1元，销售件数减少10件．

(1)、设每件商品售价定为x元（x≥40），请用含x的式子表示每月的销售量．

(2)、为了实现平均每月10000元的销售利润，并使消费者得到实惠，（1）中的售价x应定为多少元？

查看试题解析
26. 在菱形ABCD中，∠ABC＝60°，P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化．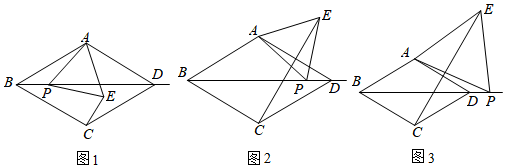

(1)、问题提出
如图1，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是， CE与CB的位置关系是．

(2)、如图2，当点E在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由．

(3)、问题解决
如图3，连湖公园有一块观赏园林区，其形状是一个边长为20m的菱形ABCD，其中∠ABC＝60°，对角线BD是一条花间小径，现计划在BD延长线上（包括D点）取点P，以AP为边长修建一个等边△APE的娱乐区，放置各类运动娱乐设施，从娱乐区顶点E再修一条直直的小路BE，为了让游客们更轻松愉快地游玩，园区还计划在BE中点处设置一个直饮水点F，求饮水点F到C点的最短距离．

查看试题解析

次数	100	200	300	400	500	600	700	800	900	1000
频率	0.60	0.30	0.50	0.36	0.42	0.38	0.41	0.39	0.40	0.40