陕西省西安市碑林区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-30 类型:期中考试
一、单选题
-
1. 图中几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如果2a=3b,那么的值为( )A、 B、 C、5 D、13. 布袋中装有2个红球、3个白球、5个黑球,它们除颜色外均相同,则从袋中任意摸出一个球是白球的概率是( )A、 B、 C、 D、4. 已知△ABC中,AC=4,BC=3,AB=5,则sinB=( )A、 B、 C、 D、5. 若x1、x2是一元二次方程x2+9x+20=0的两个根,则x1+x2的值是( )A、﹣9 B、9 C、20 D、﹣206. 如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
2. 如果2a=3b,那么的值为( )A、 B、 C、5 D、13. 布袋中装有2个红球、3个白球、5个黑球,它们除颜色外均相同,则从袋中任意摸出一个球是白球的概率是( )A、 B、 C、 D、4. 已知△ABC中,AC=4,BC=3,AB=5,则sinB=( )A、 B、 C、 D、5. 若x1、x2是一元二次方程x2+9x+20=0的两个根,则x1+x2的值是( )A、﹣9 B、9 C、20 D、﹣206. 如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( ) A、4 B、6 C、8 D、107. 如图,A,B是反比例函数y= 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A、4 B、6 C、8 D、107. 如图,A,B是反比例函数y= 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )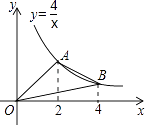 A、4 B、3 C、2 D、18. 二次函数 的图象过 四个点,下列说法一定正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则
A、4 B、3 C、2 D、18. 二次函数 的图象过 四个点,下列说法一定正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则二、填空题
-
9. 若 ,则锐角α=.10. 抛物线y=﹣2x2+4的顶点坐标为 .11. 已知一元二次方程的两根是m,n,则= .12. 已知:点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)是函数y=﹣图象上的三点,且x1<0<x2<x3 , 则y1、y2、y3的大小关系是 .13. 在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 , AB=3,则AF的长为 .

三、解答题
-
14. 解一元二次方程:15. 计算:()0+|﹣|×tan60°﹣6 .16. 解分式方程17. 如图,已知 , 请用尺规作图,在上找一点 , 使得(保留作图痕迹,不写作法).
 18. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .
18. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .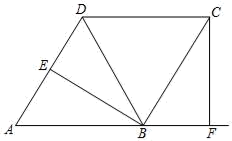 (1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.19. 为落实校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.(1)、求y与x之间的函数关系式;(2)、如果要求篮球的个数不少于排球个数的3倍,应如何购买,才能使总费用最少?最少费用是多少元?20. 在一个不透明的口袋中装有4张形状、大小相同的纸牌,它们分别标有数字1、2、3、4,随机地摸出一张纸牌,记下数字,然后放回,洗匀后再随机摸出一张纸牌并记下数字.(1)、计算两次摸出的纸牌上数字之和为6的概率;(2)、甲、乙两个人进行游戏,如果两次摸出纸牌上数字之和为奇数,则甲胜;如果两次摸出纸牌上数字之和为偶数,则乙胜.这是个公平的游戏吗?请说明理由.21. 如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20 m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.
(1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.19. 为落实校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.(1)、求y与x之间的函数关系式;(2)、如果要求篮球的个数不少于排球个数的3倍,应如何购买,才能使总费用最少?最少费用是多少元?20. 在一个不透明的口袋中装有4张形状、大小相同的纸牌,它们分别标有数字1、2、3、4,随机地摸出一张纸牌,记下数字,然后放回,洗匀后再随机摸出一张纸牌并记下数字.(1)、计算两次摸出的纸牌上数字之和为6的概率;(2)、甲、乙两个人进行游戏,如果两次摸出纸牌上数字之和为奇数,则甲胜;如果两次摸出纸牌上数字之和为偶数,则乙胜.这是个公平的游戏吗?请说明理由.21. 如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20 m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.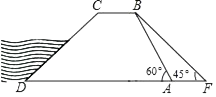 22. 某商场经销某种商品,每件成本为40元,经市场调研,当售价为50元时,可销售200件;售价每降低1元,销售量将增加10件,如果降价后该商店销售这种商品盈利1250元,问每件售价定为多少元?23. 如图,直线y=k1x+b与反比例函数y=的图象相交于点A、B,与x轴交于点C,其中点A的坐标为(﹣2,4),点B的横坐标为﹣4
22. 某商场经销某种商品,每件成本为40元,经市场调研,当售价为50元时,可销售200件;售价每降低1元,销售量将增加10件,如果降价后该商店销售这种商品盈利1250元,问每件售价定为多少元?23. 如图,直线y=k1x+b与反比例函数y=的图象相交于点A、B,与x轴交于点C,其中点A的坐标为(﹣2,4),点B的横坐标为﹣4 (1)、试确定反比例函数的表达式;(2)、求C的坐标.24. 已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)、试确定反比例函数的表达式;(2)、求C的坐标.24. 已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D. (1)、求此二次函数解析式;(2)、连接AC、CD、DB,求S四边形ACDB;(3)、在该抛物线上是否存在点P,使得S△ABP=S四边形ACDB?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.25. 问题探究:
(1)、求此二次函数解析式;(2)、连接AC、CD、DB,求S四边形ACDB;(3)、在该抛物线上是否存在点P,使得S△ABP=S四边形ACDB?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.25. 问题探究: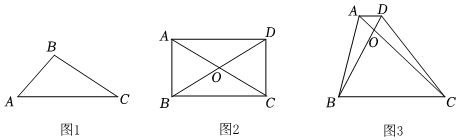 (1)、如图1,已知线段AB=2,AC=4,连接BC,则三角形ABC面积最大值是;(2)、如图2,矩形ABCD,对角线AC、BD相交于点O,且AC+BD=16,求矩形ABCD面积最大值;(3)、如图3,在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,且∠AOB=120°.若AC+BD=10,则四边形ABCD的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(1)、如图1,已知线段AB=2,AC=4,连接BC,则三角形ABC面积最大值是;(2)、如图2,矩形ABCD,对角线AC、BD相交于点O,且AC+BD=16,求矩形ABCD面积最大值;(3)、如图3,在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,且∠AOB=120°.若AC+BD=10,则四边形ABCD的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.