陕西省渭南市韩城市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程 $x^{2} - 8 x - 1 = 0$ ，配方后可变形为（）

A、 ${(x - 4)}^{2} = 17$ B、 ${(x - 4)}^{2} = 18$ C、 ${(x - 8)}^{2} = 1$ D、 ${(x - 4)}^{2} = 1$

查看试题解析
3. 如图，点 $A$ ， $B$ ， $C$ 是 $⊙ O$ 上的三个点，若 $∠ A O B = 76 °$ ，则 $∠ C$ 的度数为（）

A、76° B、38° C、24° D、33°

查看试题解析
4. 如图，将△AOB绕点O按逆时针方向旋转60°后得到△COD，若∠AOB＝15°，则∠AOD的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
5. 二次函数 $y = m x^{2} + (m + 2) x + \frac{1}{2} m + 1$ 的图象与x轴只有一个交点，则m的值为（）

A、0 B、0或2 C、2或 $- 2$ D、 $- 2$

查看试题解析
6. 如图，AB为⊙O直径，BC＝8，AC＝6，CD平分∠ACB，则AD＝（）

A、5 B、6 C、 $5 \sqrt{2}$ D、 $2 \sqrt{5}$

查看试题解析
7. 某县食品厂生产一种饮料，平均每天售出20箱，每箱盈利32元．为了减少库存，食品厂决定降价销售，如果每箱降价1元，则每天可多销售5箱，若要保证盈利1215元，设每箱降价 $x$ 元，则根据题意可列方程为（）

A、 $(32 - x) (20 + 5 x) = 1215$ B、 $(32 + x) (20 + 5 x) = 1215$ C、 $(32 - x) (20 - 5 x) = 1215$ D、 $(32 + x) (20 - 5 x) = 1215$

查看试题解析
8. 已知二次函数y＝ax²+bx+c的y与x的部分对应值如表：

x

﹣1

0

2

3

4

y

5

0

﹣4

﹣3

0

下列结论正确的是（）

A、抛物线的开口向下 B、抛物线的对称轴为直线x＝2 C、当0≤x≤4时，y≥0 D、若A（x₁ ， 2），B（x₂ ， 3）是抛物线上两点，则x₁ $<$ x₂

查看试题解析

二、填空题

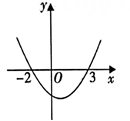
9. 若关于x的一元二次方程 $x^{2} + 2 a x + 3 b = 0$ 的一个根为3，则 $2 a + b =$ .

查看试题解析
10. 在平面直角坐标系中，已知点 $A (m ， - 3)$ 与点 $B (4 ， n)$ 关于原点对称．则 ${(m + n)}^{2021} =$ ．

查看试题解析
11. 二次函数 $y = (m + 3) x^{2} + 3 x + m^{2} - 9$ 的图象经过原点，则 $m =$ ．

查看试题解析
12. 如图是二次函数 $y = a x^{2} + b x + c$ 的图象，则由图象可知，当函数值y小于0时，x的取值范围是．

查看试题解析
13. 如图，⊙O的直径 $A B = 16$ ，半径 $O C ⊥ A B$ ， E为 $O C$ 的中点， $D E ⊥ O C$ ，交⊙O于点D，过点D作 $\begin{array}{l} D F ⊥ A B \end{array}$ 于点F．若 P为直径AB上一动点，则 $P C + P D$ 的最小值为．

查看试题解析

三、解答题

14. 解方程： $x^{2} + 4 x - 3 = 0$

查看试题解析
15. $△ A B C$ 在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位．

(1)、画出 $△ A B C$ 关于原点O的中心对称图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、在（1）的条件下，请分别写出点A、B、C的对应点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标．

查看试题解析
16. 已知关于x的一元二次方程 $m x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，求m的取值范围.

查看试题解析
17. 已知如图，AB是⊙O的直径，C、D是圆上的两点，且 $∠ C D B = 2 ∠ C B D$ ，若 $∠ D B A = 30 °$ ，求 $∠ A D C$ 的度数.

查看试题解析
18. 如图，在等腰直角 $△ A B C$ 中， $∠ A B C = 90 °$ ，点D在AC上，将 $△ A B D$ 绕顶点B沿顺时针方向旋转90°后得到 $△ C B E$ ，试判断 $△ D E C$ 的形状，并说明理由．

查看试题解析
19. 已知某企业2020年3月份的口罩产量是500万只，4月份的产量比3月份有所增长.5月份新冠疫情有所好转，口罩产量降为420万只.若两次产量变化的百分率相同，求这个百分率.

查看试题解析
20. 如图， $A B$ 是半圆O的直径，C，D是半圆O上的两点，且 $O D / / B C$ ， $O D$ 与 $A C$ 交于点E．若 $∠ B = 70 °$ ，求 $∠ C A D$ 的度数．

查看试题解析
21. 已知抛物线 $y = x^{2} + 2 x + c$ 经过点 $(2 ， 5)$ ．

(1)、求该抛物线的解析式及其顶点坐标；

(2)、若将该抛物线向下平移2个单位，再向左平移2个单位后得到新抛物线，求新抛物线相应的函数解析式，并判断点 $(- 1 ， 2)$ 是否在新抛物线上．

查看试题解析
22. 如图是一张长12cm，宽10cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积是24cm²的有盖的长方体铁盒，求剪去的正方形的边长.

查看试题解析
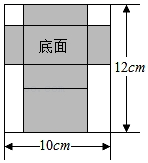23. 如图，已知二次函数的图象与x轴交于A，B两点（A点在B点的左侧），与y轴交于点 $D (0 ， 4)$ ，其顶点C的坐标为 $(4 ， - \frac{4}{3})$ ．

(1)、求这个二次函数的解析式以及A，B两点的坐标；

(2)、连接AC、CB、BD、AD，求四边形ACBD的面积．

查看试题解析
24. 如图，有一座圆弧形拱桥，桥下水面宽度 $A B$ 为 $16 m$ ，拱高 $C D$ 为 $4 m$ ．

(1)、求拱桥的半径；

(2)、有一艘宽为 $10 m$ 的货船，船舱顶部为长方形，并高出水面 $2 m$ ，则此货船是否能顺利通过此圆弧形拱桥，并说明理由．

查看试题解析
25. 由于秋冬季节容易引发呼吸道疾病，越来越多的家庭选择购买空气净化器来预防呼吸道疾病，某商场的一款空气净化器特别畅销．已知进价是每台20元，根据市场调查发现，每月的销售量y（台）与售价x（元/台）满足 $y = - 10 x + 1200$ 的一次函数关系．

(1)、某月该商场出售这种空气净化器获得了21000元的利润，该空气净化器的售价是多少？

(2)、若某月该商场这种空气净化器的售价不大于55元/台，该商场销售这种空气净化器获得的最大利润是多少？

查看试题解析
26. 如图，已知抛物线 $y = - x^{2} + 2 x + 3$ 与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接BC．

(1)、求A、B、C三点的坐标；

(2)、若点P为线段BC上的一点（不与B、C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当线段PM的长度最大时，求点M的坐标；

(3)、在（2）的条件下，当线段PM的长度最大时，在抛物线的对称轴上有一点Q，使得△CNQ为直角三角形，直接写出点Q的坐标．

查看试题解析

x	﹣1	0	2	3	4
y	5	0	﹣4	﹣3	0