陕西省宝鸡市凤翔县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列命题中正确的是（）

A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是矩形 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的平行四边形是矩形

查看试题解析
2. 下列图形中不一定相似的是（）

A、两个矩形 B、两个圆 C、两个正方形 D、两个等边三角形

查看试题解析
3. 下列方程中是关于x的一元二次方程的是（）

A、x²+ $\frac{1}{x^{2}}$ ＝1 B、（x﹣1）（x+2）＝1 C、ax²+bx+c＝0 D、3x²﹣5xy﹣5y²＝0

查看试题解析
4. 已知菱形的边长为6，一个内角为60°，则菱形较长的对角线长是（）

A、 $3 \sqrt{3}$ B、 $6 \sqrt{3}$ C、3 D、6

查看试题解析
5. 方程x²＝2x的根是（　　）

A、x＝2 B、x＝0 C、x₁＝0，x₂＝2 D、x₁＝0，x₂＝﹣2

查看试题解析
6. 如图，直线l₁∥l₂∥l₃ ，若AB=2，BC=3，DE=1，则EF的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、6 D、 $\frac{1}{6}$

查看试题解析
7. 关于四边形ABCD有以下4个条件：①两组对边分别平行；②两条对角线互相平分；③两条对角线互相垂直；④一组邻边相等．从中任取2个条件，能得到四边形ABCD是菱形的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{6}$

查看试题解析
8. 七巧板是我国古代的一种拼板玩具，它已经有两千五百多年的历史了.如图所示的七巧板中，若平行四边形BEFG的周长等于10，则△BCD的周长等于（）

A、10 B、15 C、20 D、25

查看试题解析

二、填空题

9. 若 $a ， b$ 是方程 $x^{2} - 2 x - 3 = 0$ 的两个实数根，则 $a^{2} + b^{2} =$ ．

查看试题解析
10. 已知 $\frac{a + b}{c}$ ＝ $\frac{a + c}{b}$ ＝ $\frac{b + c}{a}$ ＝k，则k的值是．

查看试题解析
11.
如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为 cm² ．

查看试题解析
12. 一个口袋中有25个球，其中红球、黑球、黄球若干个，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计口袋中的黄球约有个．

查看试题解析
13. 如图，在平面直角坐标系中，O为原点，四边形OABC是矩形，A（-10，0），C（0，3），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标是 .

查看试题解析

三、解答题

14. 解方程：x²﹣2 $\sqrt{5}$ x+2＝0．

查看试题解析
15. 解方程：x（5x+4）＝5x+4．

查看试题解析
16. 已知a：b：c＝3：2：1，且a﹣2b+3c＝4，求2a+3b﹣4c的值．

查看试题解析
17. 如图，在平行四边形ABCD中，点P是AB边上一点（不与A，B重合），过点P作PQ⊥CP，交AD边于点Q，且∠QPA＝∠PCB．
求证：四边形ABCD是矩形．

查看试题解析
18. 若关于x的一元二次方程(m-1) $x^{2}$ +2x+ $m^{2}$ -1=0的常数项为0，求m的值是多少？

查看试题解析
19. 如图，已知四边形ABCD是矩形，尺规作图，求作正方形BECF，使得顶点E在矩形ABCD内．

查看试题解析
20. 已知a是方程x²﹣x﹣1＝0的一个根，求 $\frac{a^{2} - a}{(a^{2} - a)^{2} - 1 + \sqrt{3}}$ 的值．

查看试题解析
21. 如图，矩形 $A B C D$ 中， $A C$ 与 $B D$ 交于点 $O ， B E ⊥ A C ， C F ⊥ B D$ ，垂足分别为 $E ， F .$ 求证： $B E ＝ C F$ .

查看试题解析
22. 汽车站水果批发市场经销一种水果，如果每千克盈利10元，每天可售出500千克经市场调查发现，在进货价不变的情况下，若每千克这种水果在原售价的基础上每涨价1元，日销售量将减少20千克．如果市场每天销售这种水果盈利了6000元，同时顾客又得到了实惠，那么每千克这种水果涨了多少元？

查看试题解析
23. 小明想给小东打电话，但忘记了电话号码中的一位数字，只记得号码是284□9456（□表示忘记的数字）

(1)、若小明从0至9的自然数中随机选取一个数字放在□位置，求他正确拨打小东电话的概率；

(2)、若□位置的数字是不等式组 ${\begin{array}{l} 2 x - 11 > 0 \\ x \leq \frac{1}{2} x + 4 \end{array}$ 的整数解，求□可能表示的数字．

查看试题解析
24. 为弘扬“东亚文化”，某单位开展了“东亚文化之都”演讲比赛，在安排1位女选手和3位男选手的出场顺序时，采用随机抽签方式．

(1)、请直接写出第一位出场是女选手的概率；

(2)、请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果，并求出他们都是男选手的概率．

查看试题解析
25. 如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．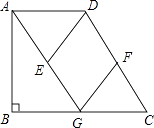

(1)、求证：四边形DEGF是平行四边形；

(2)、当点G是BC的中点时，求证：四边形DEGF是菱形．

查看试题解析
26. 如图，在Rt△ABC中，∠C＝90°，AC＝20，∠A＝60°．点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动，同时点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点P、Q运动的时间是t秒．过点P作PM⊥BC于点M，连接PQ、QM．

(1)、请用含有t的式子填空：AQ＝， AP＝， PM＝；

(2)、是否存在某一时刻使四边形AQMP为菱形？如果存在，求出相应的t值；如果不存在，说明理由．

查看试题解析