吉林省长春市朝阳区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
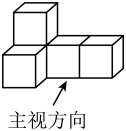
1. 若数轴上的点A、B、C、D表示的数分别是、、1、 , 则距离原点最远的点是( )A、点A B、点B C、点C D、点D2. 2021年5月15日,我国“天问一号”探测器在火星成功着陆.火星具有和地球相近的环境,与地球最近时候的距离约 .将数字55000000用科学记数法表示为( )A、 B、 C、 D、3. 由5个相同的小正方体搭成的几何体如图所示,则它的左视图是( )
 A、
A、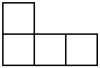 B、
B、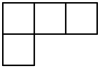 C、
C、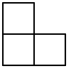 D、
D、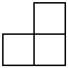 4. 下列计算中,正确的是( )A、 B、 C、 D、5. 用代数式表示“ 的3倍与 的差的平方”正确的是( )A、 B、 C、 D、6. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能符合题意解释这一现象的数学知识是( )
4. 下列计算中,正确的是( )A、 B、 C、 D、5. 用代数式表示“ 的3倍与 的差的平方”正确的是( )A、 B、 C、 D、6. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能符合题意解释这一现象的数学知识是( ) A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直7. 如图,在灯塔O处观测到轮船A位于北偏西66°的方向,轮船B在OA的反向延长线的方向上,同时轮船C在东南方向,则∠BOC的大小为( )
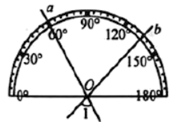
A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直7. 如图,在灯塔O处观测到轮船A位于北偏西66°的方向,轮船B在OA的反向延长线的方向上,同时轮船C在东南方向,则∠BOC的大小为( ) A、45° B、31° C、24° D、21°8. 如图,射线OC、OD把平角∠AOB三等分,OE平分∠AOC,OF平分∠BOD,下列说法正确的是( )
A、45° B、31° C、24° D、21°8. 如图,射线OC、OD把平角∠AOB三等分,OE平分∠AOC,OF平分∠BOD,下列说法正确的是( ) A、图中只有两个120°的角 B、图中只有∠DOE是直角 C、图中∠AOC的补角有3个 D、图中∠AOE的余角有2个
A、图中只有两个120°的角 B、图中只有∠DOE是直角 C、图中∠AOC的补角有3个 D、图中∠AOE的余角有2个二、填空题
-
9. 比较大小: (填“ ”或“ ”).10. 某市三年前人均年收入为m元,预计今年人均年收入是三年前的2倍多500元,则今年人均年收入预计将达到元.11. 如图,直线 、 相交于点 ,将量角器的中心与点 重合,发现表示 的点在直线 上,表示 的点在直线 上,则 .
 12. 一个正方体的平面展开图如图所示。若将展开图折叠成正方体后,相对面上所标的两个数互为相反数,则的值为 .
12. 一个正方体的平面展开图如图所示。若将展开图折叠成正方体后,相对面上所标的两个数互为相反数,则的值为 . 13. 如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若 , 则∠CBD的大小为度.
13. 如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若 , 则∠CBD的大小为度. 14. 如图,从左至右,第1个图案中有6个等边三角形和6个正方形,第2个图案中有10个等边三角形和11个正方形,第3个图案中有14个等边三角形和16个正方形,……即从第2个图案开始,每个图案比前一个图案多4个等边三角形和5个正方形,则第n个图案中等边三角形和正方形的个数之和为个.
14. 如图,从左至右,第1个图案中有6个等边三角形和6个正方形,第2个图案中有10个等边三角形和11个正方形,第3个图案中有14个等边三角形和16个正方形,……即从第2个图案开始,每个图案比前一个图案多4个等边三角形和5个正方形,则第n个图案中等边三角形和正方形的个数之和为个.
三、解答题
-
15. 计算: .16. 化简: .17. 如图,在的正方形网格中,每个小正方形的顶点称为格点.点A、点B、点C都在格点上,利用学具完成下列作图.
 (1)、作直线AB.(2)、过点C作直线AB的垂线CD,垂足为点D.(3)、过点C作直线AB的平行线CE.18. 某仓库一周内进出货物的吨数如下(“+”表示进库,“一”表示出库):
(1)、作直线AB.(2)、过点C作直线AB的垂线CD,垂足为点D.(3)、过点C作直线AB的平行线CE.18. 某仓库一周内进出货物的吨数如下(“+”表示进库,“一”表示出库):, , , , , ,
(1)、经过这7天后,仓库里的货物是增多了还是减少了?增多或减少了多少吨?(2)、如果进出仓库的货物装卸费都是每吨5元,求该仓库这7天共支付的装卸费用.19. 先化简,再求值: , 其中 , .20. 如图,A、B是直线MN上的两个点,且不重合,分别过点A、B作直线MN的垂线AC、BD,点C、D在直线MN的同侧.若 , , 则AC与BD平行吗?AE与BF平行吗?完成下面的解答过程,并填空(理由或数学式).
解:∵ , ( )
∴( )
∵ ,
∴( )
∴ ,
同理可得 ,
∵ , ,
∴( )( )
∴( )=∠2.
∴( ).
21. 某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.该厂在开展促销活动期何,向客户提供两种优惠方案:方案一:买一套西装送一条领带.
方案二:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条().
(1)、若该客户按方案一购买,需付款元 用含x的代数式表示 .若该客户按方案二购买,需付款元 用含x的代数式表示 .
(2)、若 , 且该客户只选择其中一种方案购买西装和领带,通过计算说明按哪种方案购买较为合算?22. 【教材呈现】下图是华师版七年级上册数学教材第176页的部分内容.有了“两直线平行,同位角相等”,我们就能用推理的方法得出“两条平行线被第三条直线所截,内错角相等”.
如图5.2.13,平行线a、b被直线l所截,我们将∠1的对顶角记为∠3…

 (1)、小明根据提示,写出了如下证明过程.根据小明的推理过程,在括号内填写理由.
(1)、小明根据提示,写出了如下证明过程.根据小明的推理过程,在括号内填写理由.∵ ,
∴( ).
∵( ),
∴( ).
(2)、如图①, . 若 , 则∠2的余角的大小为度.(3)、如图②, , , 若 , 求∠D的大小.23. 如图,点B在线段AC上,且 , . 动点P从点A出发,沿AC以每秒3个单位长度的速度向终点C匀速运动;同时动点Q从点C出发,沿CA以每秒2个单位长度的速度向终点A匀速运动。设点P的运动时间为t(s). (1)、线段AB、BC的中点之间的距离为 ,(2)、当点P到点C时,求PQ的长.(3)、求PQ的长(用含t的代数式表示)(4)、设时,直接写出t的值.24.(1)、【阅读理解】题目:如图①,∠ABE和∠DCE的边AB与CD互相平行,边BE与CE交于点E.若 , , 求∠BEC的度数.
(1)、线段AB、BC的中点之间的距离为 ,(2)、当点P到点C时,求PQ的长.(3)、求PQ的长(用含t的代数式表示)(4)、设时,直接写出t的值.24.(1)、【阅读理解】题目:如图①,∠ABE和∠DCE的边AB与CD互相平行,边BE与CE交于点E.若 , , 求∠BEC的度数.
老师在黑板中写出了部分求解过程,请你完成下面的求解过程,并填空(理由或数学式).
解:如图②,过点E作 .
∴( ).
∵ ,
∴ .
∵( ),
∴( ).
∴( )
∵ ,
∴ .
∴( )°
(2)、【问题迁移】如图③,D、E分别是∠ABC边AB、BC上的点,在直线DE的右侧作DE的平行线分别交边BC、AB于点F、G.P是线段DG上一点,连结PE、PF.若 , , 求∠EPF的度数.(3)、【拓展应用】如图④,D、E分别是∠ABC边AB、BC上的点,在直线DE的右侧作DE的平行线分别交边BC、AB于点F、G.P是射线DG上一点,连结PE、PF.若 , , 直接写出∠EPF与、之间的数量关系.