吉林省松原市乾安县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. 数轴上的点A表示的数可以是( )
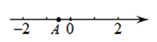 A、-1.5 B、 C、0.5 D、1.52. 我国与“一带一路”沿线国家货物贸易进出口总额达到13400亿美元,用科学记数法表示:13400应为( )A、 B、 C、 D、3. 如图,下面的平面图形绕轴旋转一周,可以得到圆柱体的是( )A、
A、-1.5 B、 C、0.5 D、1.52. 我国与“一带一路”沿线国家货物贸易进出口总额达到13400亿美元,用科学记数法表示:13400应为( )A、 B、 C、 D、3. 如图,下面的平面图形绕轴旋转一周,可以得到圆柱体的是( )A、 B、
B、 C、
C、 D、
D、 4. 若∠A=130°,∠B=50°,则下列说法中错误的是( )A、∠A与∠B互补. B、∠B比∠A小80°. C、∠A与∠B互余. D、∠A是钝角,∠B是锐角.5. 某一时刻,时钟上显示的时间是9点30分,则此时时针与分针的夹角是( )A、75°. B、90°. C、105°. D、120°.6. 若a,b在数轴上的位置如图所示,则下列结论正确的是( )
4. 若∠A=130°,∠B=50°,则下列说法中错误的是( )A、∠A与∠B互补. B、∠B比∠A小80°. C、∠A与∠B互余. D、∠A是钝角,∠B是锐角.5. 某一时刻,时钟上显示的时间是9点30分,则此时时针与分针的夹角是( )A、75°. B、90°. C、105°. D、120°.6. 若a,b在数轴上的位置如图所示,则下列结论正确的是( )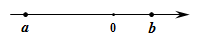 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 某运动员在东西走向的公路上练习跑步,跑步情况记录如下(向东为正,单位:米):1000, , 1100, , 1400,该运动员跑的路程共为米.8. 某商场对原单价为元的书包打8折出售,则该种书包的现在单价为元.9. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A,B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中 蕴含的数学道理是 .
 10. 如果x=8是方程的一个解,则k= ,11. 数轴上表示整数的点称为整点.某数轴的单位长度是1cm,若在这个数轴上随意画出一条长为2021cm的线段AB,则盖住的整点的个数是 .12. 如图,长度为12cm的线段AB的中点是点M,点C在线段MB上,且 , 则线段AC的长为 .
10. 如果x=8是方程的一个解,则k= ,11. 数轴上表示整数的点称为整点.某数轴的单位长度是1cm,若在这个数轴上随意画出一条长为2021cm的线段AB,则盖住的整点的个数是 .12. 如图,长度为12cm的线段AB的中点是点M,点C在线段MB上,且 , 则线段AC的长为 .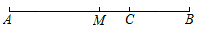 13. 如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于度.
13. 如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于度.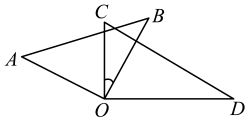 14. 观察下列图形,它们是按一定规律排列的,依照此规律,第5个图形有个太阳.
14. 观察下列图形,它们是按一定规律排列的,依照此规律,第5个图形有个太阳.
三、解答题
-
15. 计算: .16. 已知与互为相反数,与互为倒数,的平方等于4,试求的值.17. 先化简,再求值: , 其中 , .18. 下面是小明解方程的过程,请你仔细阅读,并解答所提出的问题:
解:去括号,得
. (第一步)
移项,得
. (第二步)
合并同类项,得
. (第三步)
系数化为1,得
. (第四步)
(1)、该同学解答过程从第步开始出错,错误原因是;(2)、写出正确的解答过程.19. 如图,已知平面内的四点、、、 . 请你按下列语句画图: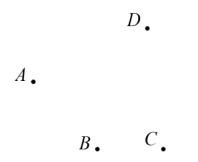 (1)、连接(2)、作射线(3)、作直线(4)、线段与相交于点 .(5)、反向延长到 , 使 .20. 如图,已知点B在线段AC上,AB=8 cm,BC=10 cm,点P,Q分别为AB,AC的中点.
(1)、连接(2)、作射线(3)、作直线(4)、线段与相交于点 .(5)、反向延长到 , 使 .20. 如图,已知点B在线段AC上,AB=8 cm,BC=10 cm,点P,Q分别为AB,AC的中点.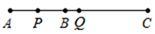 (1)、线段AC的长为cm,线段PC的长为cm;(2)、求线段PQ的长.21. 有一些相同的房间需要粉刷,一天3名师傅去粉刷8个房间,结果其中有40m2墙面未来得及刷;同样的时间内5名徒弟粉刷了9个房间的墙面.每名师傅比徒弟一天多刷30m2的墙面.(1)、求每个房间需要粉刷的墙面面积;(2)、张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需要几天完成.22. 阳信县城某通信公司,给客户提供手机通话有以下两种计费方式(用户可任选其一):
(1)、线段AC的长为cm,线段PC的长为cm;(2)、求线段PQ的长.21. 有一些相同的房间需要粉刷,一天3名师傅去粉刷8个房间,结果其中有40m2墙面未来得及刷;同样的时间内5名徒弟粉刷了9个房间的墙面.每名师傅比徒弟一天多刷30m2的墙面.(1)、求每个房间需要粉刷的墙面面积;(2)、张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需要几天完成.22. 阳信县城某通信公司,给客户提供手机通话有以下两种计费方式(用户可任选其一):(A)每分钟通话费0.1元;(B)月租费20元,另外每分钟收取0.05元.
(1)、该用户12月份通话多少分钟时,两种方式的费用一样?(2)、请说明如何选择计费方式才能节省费用?(直接写出结果即可)23. 用“⊕”定义一种新运算:对于任意有理数和 , 规定 .如: .
(1)、则的值为;(2)、若 , 求的值.24. 已知是上的一点,是直角,平分 .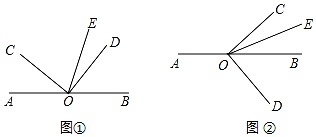 (1)、如图①,若 , 求的度数;(2)、将图①中的绕顶点顺时针旋转至图②的位置,猜想与之间存在什么样的数量关系,写出你的结论,并说明理由.25. 某学校组织七年级学生参加研学活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.(1)、求该校此次参加研学活动的学生有多少人?(2)、若单独租用60座的客车,需租辆;(3)、已知45座客车的日租金为每辆1 000元,60座客车的日租金为每辆1 200元,该校单独租用哪种车更合算?26. 如图,在数轴上有 , 两点,所表示的数分别为 , , 点以每秒5个单位长度的速度向右运动,同时点以每秒3个单位长度的速度也向右运动,设运动时间为秒,解答下列问题:
(1)、如图①,若 , 求的度数;(2)、将图①中的绕顶点顺时针旋转至图②的位置,猜想与之间存在什么样的数量关系,写出你的结论,并说明理由.25. 某学校组织七年级学生参加研学活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.(1)、求该校此次参加研学活动的学生有多少人?(2)、若单独租用60座的客车,需租辆;(3)、已知45座客车的日租金为每辆1 000元,60座客车的日租金为每辆1 200元,该校单独租用哪种车更合算?26. 如图,在数轴上有 , 两点,所表示的数分别为 , , 点以每秒5个单位长度的速度向右运动,同时点以每秒3个单位长度的速度也向右运动,设运动时间为秒,解答下列问题: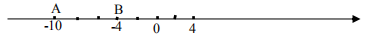 (1)、运动前线段的长为;运动1秒后线段的长为;(2)、运动秒后,点、点运动的距离分别为和;(3)、求为何值时,点和点恰好重合;(4)、在上述运动过程中,是否存在某一时刻 , 使得线段的长为4,若存在,求出的值;若不存在,请说明理由.
(1)、运动前线段的长为;运动1秒后线段的长为;(2)、运动秒后,点、点运动的距离分别为和;(3)、求为何值时,点和点恰好重合;(4)、在上述运动过程中,是否存在某一时刻 , 使得线段的长为4,若存在,求出的值;若不存在,请说明理由.