黑龙江省齐齐哈尔市依安县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. -5的倒数是A、 B、5 C、 D、-52. 若|x﹣2|+(y﹣3)2=0,则﹣x+y=( )A、1 B、0 C、﹣1 D、53. 已知 , 下列四个选项能确定点C是线段AB的中点的是( )A、 B、 C、 D、4. 将方程 去分母,结果正确的是( )A、 B、 C、 D、5. 多项式2x3﹣10x2+4x﹣1与多项式3x3﹣4x﹣5x2+3相加,化简后不含的项是( )A、三次项 B、二次项 C、一次项 D、常数项6. 如图,学校、公园、体育场在平面图上的位置分别是点O、A、B,若OB的方向是南偏东60°,∠AOB=90°,则OA的方向是( )
 A、北偏东30° B、南偏东30° C、南偏西60° D、东偏北30°7. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
A、北偏东30° B、南偏东30° C、南偏西60° D、东偏北30°7. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、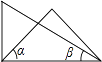 C、
C、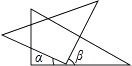 D、
D、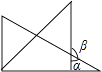 8. 某校为了丰富“阳光体育”活动,现购进篮球和足球共16个,共花了2820元,已知篮球的单价为185元,篮球是足球个数的3倍,则足球的单价为( )A、120元 B、130元 C、150元 D、140元9. 如图,由几个相同的小正方体搭成一个几何体,从上面观察该图形,得到的平面图形是( )
8. 某校为了丰富“阳光体育”活动,现购进篮球和足球共16个,共花了2820元,已知篮球的单价为185元,篮球是足球个数的3倍,则足球的单价为( )A、120元 B、130元 C、150元 D、140元9. 如图,由几个相同的小正方体搭成一个几何体,从上面观察该图形,得到的平面图形是( )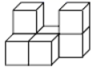 A、
A、 B、
B、 C、
C、 D、
D、 10. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
10. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( ) A、70 B、72 C、74 D、76
A、70 B、72 C、74 D、76二、填空题
-
11. 请写出一个系数为负数,次数为5的关于x、y的单项式 .12. 计算: = .13. 关于 的方程 如果是一元一次方程,则其解为 .14. 如果单项式﹣xa﹣2y2b+1与单项式7x2a﹣7y4b﹣3是同类项,则ab= .15. 如图,是小明同学在数学实践课上,所设计的正方体盒子的平面展开图,每个面上都有一个汉字,请你判断,正方体盒子上与“答”字相对的面上的字是.
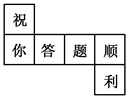 16. 如图,将一张长方形的纸片沿折痕EF翻折,使点B、C分别落在点M、N的位置,且∠AFM=∠EFM,则∠AFM=°.
16. 如图,将一张长方形的纸片沿折痕EF翻折,使点B、C分别落在点M、N的位置,且∠AFM=∠EFM,则∠AFM=°. 17. 如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n个图中正方形和等边三角形的个数之和为个.
17. 如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n个图中正方形和等边三角形的个数之和为个.
三、解答题
-
18. 计算:(1)、﹣10﹣|﹣8|÷(﹣2)×(﹣);(2)、(﹣+﹣)×12+(﹣1)2021 .19. 解方程20. 对两个任意有理数、 , 规定一种新的运算: , 例如: . 根据新的运算法则,解答下列问题:(1)、求的值;(2)、若 , 求的值.21. 如图,已知∠AOB=140°,∠COE与∠EOD互余,OE平分∠AOD.
 (1)、若∠COE=40°,求∠DOE和∠BOD;(2)、设∠COE=α,∠BOD=β,试探究α与β之间的数量关系.22. 奶奶逛超市看到如下两个超市的促销信息.
(1)、若∠COE=40°,求∠DOE和∠BOD;(2)、设∠COE=α,∠BOD=β,试探究α与β之间的数量关系.22. 奶奶逛超市看到如下两个超市的促销信息.甲超市促销信息栏:全场8.8折.
乙超市促销信息栏:不超过200元,不给予优惠;超过200元而不超过500元,全部打9折;超过500元,其中500元的部分优惠10%,超过500元的部分打8折.(注:假设两个超市相同商品的标价都一样)
(1)、当一次性购买商品的标价总额是a元时(200<a<500),甲、乙两超市实际付款分别是多少元?(2)、当标价总额是多少元时,甲、乙两超市实付款一样?(3)、奶奶两次到乙超市购物付款分别是170元和474元,若她只去一次该超市购买同样的商品,你帮助奶奶算一算可以节省多少元?23. 如图,已知数轴上的三个点 , , 对应的数分别为 , 0,3,点为数轴上任意一点,其对应的数为 . (1)、的长为;(2)、如果点到点、点的距离相等,那么的值是;(3)、数轴上是否存在点 , 使点到点、点的距离之和是8?若存在,直接写出的值;若不存在,请说明理由;(4)、如果点以每分钟1个单位长度的速度从点O向左运动,同时点和点分别以每分钟2个单位长度和每分钟3个单位长度的速度向左运动,设分钟时,点到点、点的距离相等,求的值.
(1)、的长为;(2)、如果点到点、点的距离相等,那么的值是;(3)、数轴上是否存在点 , 使点到点、点的距离之和是8?若存在,直接写出的值;若不存在,请说明理由;(4)、如果点以每分钟1个单位长度的速度从点O向左运动,同时点和点分别以每分钟2个单位长度和每分钟3个单位长度的速度向左运动,设分钟时,点到点、点的距离相等,求的值.