黑龙江省齐齐哈尔市铁锋区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 下列说法正确的是( )A、﹣的系数是﹣ B、52a2b的次数是6次 C、是多项式 D、﹣3a4b与7ba4不是同类项3. 已知有理数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
 A、a•b>0 B、a+b<0 C、|a|<|b| D、a﹣b>04. 若 是关于 的方程 的解,则 的值为( )A、1 B、-1 C、7 D、-75. 已知无论 , 取什么值,多项式的值都等于定值12,则等于( ).A、8 B、 C、2 D、6. 下列图形中,不是正方体的展开图的是( )
A、a•b>0 B、a+b<0 C、|a|<|b| D、a﹣b>04. 若 是关于 的方程 的解,则 的值为( )A、1 B、-1 C、7 D、-75. 已知无论 , 取什么值,多项式的值都等于定值12,则等于( ).A、8 B、 C、2 D、6. 下列图形中,不是正方体的展开图的是( )
A、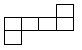 B、
B、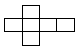 C、
C、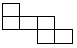 D、
D、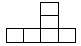 7. 若A,B,C三点共线,线段AB=10cm,BC=4cm,点E,F分别是线段AB,BC的中点,则线段EF的长( )A、14cm或6cm B、7cm C、3cm D、7cm或3cm8. 下列说法:①锐角和钝角互补;②连接两点的直线的长度叫两点之间的距离;③由mx=my,则x=y;④若∠AOC=∠AOB,则射线OC为∠AOB的平分线;⑥若平面内6条直线两两相交,则交点个数最多为15个,以上说法正确的个数是( )A、1个 B、2个 C、3个 D、4个9. 设 , 那么与的大小关系是( )A、 B、 C、 D、无法确定10. 如图,已知数轴上点A表示的数为a,点B表示的数为b,(a﹣10)2+|b+6|=0.动点P从点A出发,以每秒8个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.若点P、Q同时出发,当P、Q两点相距4个单位长度时, t的值为( )
7. 若A,B,C三点共线,线段AB=10cm,BC=4cm,点E,F分别是线段AB,BC的中点,则线段EF的长( )A、14cm或6cm B、7cm C、3cm D、7cm或3cm8. 下列说法:①锐角和钝角互补;②连接两点的直线的长度叫两点之间的距离;③由mx=my,则x=y;④若∠AOC=∠AOB,则射线OC为∠AOB的平分线;⑥若平面内6条直线两两相交,则交点个数最多为15个,以上说法正确的个数是( )A、1个 B、2个 C、3个 D、4个9. 设 , 那么与的大小关系是( )A、 B、 C、 D、无法确定10. 如图,已知数轴上点A表示的数为a,点B表示的数为b,(a﹣10)2+|b+6|=0.动点P从点A出发,以每秒8个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.若点P、Q同时出发,当P、Q两点相距4个单位长度时, t的值为( ) A、3 B、5 C、3或5 D、1或
A、3 B、5 C、3或5 D、1或二、填空题
-
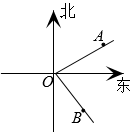
11. 据中国电影数据信息网消息,截止到 年 月 日,诠释伟大抗美援朝精神的电影 长津湖 累计票房已达 亿元.将 亿元用科学记数法表示元.12. 若n= , abc<0,则n的值为 .13. 若关于x的方程(m﹣5)x|m|﹣4+18=0是一元一次方程,则m= .14. 若x2+3x的值为8,则3x2+9x﹣2的值为 .15. 如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东62°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的余角的度数是 .
 16. 已知在同一平面内,OD平分∠AOC,∠AOB=30°,射线OC在∠AOB的外部,若∠BOD=50°,则∠AOC为 度.17. 在庆祝建党“100周年”的活动中,围棋社的同学用棋子摆成如图所示的“100”图案,其中第1个“100”图案用11个棋子,第3个“100”图案用21个棋子……按这种规律,第n个“100”图案用 个棋子.
16. 已知在同一平面内,OD平分∠AOC,∠AOB=30°,射线OC在∠AOB的外部,若∠BOD=50°,则∠AOC为 度.17. 在庆祝建党“100周年”的活动中,围棋社的同学用棋子摆成如图所示的“100”图案,其中第1个“100”图案用11个棋子,第3个“100”图案用21个棋子……按这种规律,第n个“100”图案用 个棋子.
三、解答题
-
18. 计算:(1)、﹣12021﹣[(﹣2)2÷×6+4];(2)、132°25′﹣55°43′20″.19. 解方程:(1)、3x+2=4(2x+3);(2)、﹣1.20. 已知:a与b互为相反数且a、b均不为零,c是最大的负整数,d是倒数等于本身的数,x是平方等于9的数,试求x++2c﹣21. “⊗”表示一种运算符号,其定义是a⊗b=﹣2a+b.例如3⊗7=﹣2×3+7.(1)、若x⊗(﹣5)=﹣3,则x=;(2)、在(1)的条件下,化简多项式3x2﹣x3﹣(6x2﹣7x)﹣2(x3﹣3x2﹣4x),并求出它的值.22. 如图,点C为线段AB上一点,点D为BC的中点,AC=4CD,AB=12cm,求线段AC的长度.
 23. 如图,小明将两块完全相同的含60°角的直角三角板的直角顶点C叠放在一起,保持△BCD不动(1)、问题发现:
23. 如图,小明将两块完全相同的含60°角的直角三角板的直角顶点C叠放在一起,保持△BCD不动(1)、问题发现: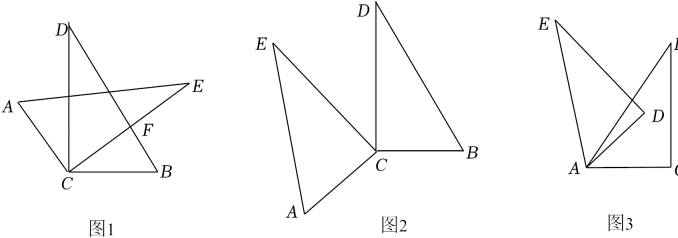
如图1,若∠DCE=50°,则∠ACB=;若∠ACB=140°,则∠DCE=°;
(2)、问题探究:①当直角三角形ACE绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系为 ▲ ;
②当△ACE绕直角顶点C旋转到如图2的位置时,图1中∠ACB与∠DCE的数量关系是否仍然成立?请说明理由.
(3)、问题拓展:如图3,将两块直角三角板重叠在一起,将直角三角形ADE绕60°角的顶点A逆时针旋转到如图所示的位置,∠EAC与∠BAD有怎样的数量关系?请直接写出你的结论.
24. 综合与探究为了防治“新型冠状病毒”,某中学拟向厂家购买消毒剂和红外线测温枪,积极做好师生的测温和教室消毒工作.若按原价购买一瓶消毒剂和一支红外线测温枪共需要210元,一支测温枪的价格比一瓶消毒剂的价格的9倍还多10元
(1)、每瓶消毒剂的价格为元;每支测温枪的价格为元;(2)、由于采购量大,商家推出两种优惠方案(如表):购买方案
红外线测温枪
消毒剂
买赠
A
9折
7折
买一支红外线测温枪
送1瓶消毒剂
B
7折
8折
无
已知学校有30个班级,计划每班配置1支红外线测温枪和x瓶消毒剂,当x为何值时两种方案购买所需的总费用相同?
(3)、当x=20时,学校选择上述哪一种方案总费用最低?请直接写出答案.