黑龙江省齐齐哈尔市龙沙区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. -2020的相反数是( )A、2020 B、-2020 C、 D、-2. 下面的四个几何图形中,表示平面图形的是( )A、
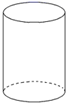 B、
B、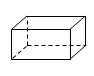 C、
C、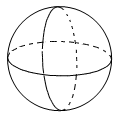 D、
D、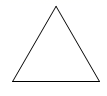 3. 连云港市某天最高气温9℃,最低气温﹣2℃,那么这天的日温差是( )A、7℃ B、﹣11℃ C、﹣7℃ D、11℃4. 下列运用等式性质正确的是( )A、如果a=b,那么a+c=b-c B、如果ac=bc,那么a=b C、如果= , 那么a=b D、如果a2=ab,那么a=b5. 若有理数a,b满足=0,则a+b的值为( )A、1 B、﹣1 C、5 D、﹣56. 单项式﹣的系数与次数分别为( )A、﹣2,3 B、﹣ , 2 C、﹣ , 3 D、 , 37. 解方程 , 去分母正确的是( )A、3(x-1)-2(2x+1)=6 B、3(x-1)-2(2x+1)=1 C、2(x-1)-3(2x+1)=6 D、3x-1-4x-1=68. 有理数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( )
3. 连云港市某天最高气温9℃,最低气温﹣2℃,那么这天的日温差是( )A、7℃ B、﹣11℃ C、﹣7℃ D、11℃4. 下列运用等式性质正确的是( )A、如果a=b,那么a+c=b-c B、如果ac=bc,那么a=b C、如果= , 那么a=b D、如果a2=ab,那么a=b5. 若有理数a,b满足=0,则a+b的值为( )A、1 B、﹣1 C、5 D、﹣56. 单项式﹣的系数与次数分别为( )A、﹣2,3 B、﹣ , 2 C、﹣ , 3 D、 , 37. 解方程 , 去分母正确的是( )A、3(x-1)-2(2x+1)=6 B、3(x-1)-2(2x+1)=1 C、2(x-1)-3(2x+1)=6 D、3x-1-4x-1=68. 有理数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( ) A、a+b>0 B、a﹣b>0 C、ab>0 D、<09. 如图,∠AOC=∠BOD=80 ,如果∠AOD=140 ,那∠BOC等于 ( )
A、a+b>0 B、a﹣b>0 C、ab>0 D、<09. 如图,∠AOC=∠BOD=80 ,如果∠AOD=140 ,那∠BOC等于 ( ) A、20 B、30 C、50 D、4010. 下列各式去括号错误的有( )
A、20 B、30 C、50 D、4010. 下列各式去括号错误的有( )①;②;③;④
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 月球距离地球平均为384000000米,数字384000000用科学记数法表示为 .12. 已知a=﹣7,b=2,则|a|﹣|﹣b|= .13. 某服装店新开张,第一天销售服装a件,第二天比第一天少销售10件,第三天的销售量是第二天的2倍多7件,则第三天销售了 件.14. 按如图所示程序工作,如果输入的数是1,那么输出的数是 .
 15. 如图,小明将一个正方形纸剪出一个宽为 的长条后,再从剩下的长方形纸片上剪去一个宽为 的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为 .
15. 如图,小明将一个正方形纸剪出一个宽为 的长条后,再从剩下的长方形纸片上剪去一个宽为 的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为 . 16. 已知A、B、C三点在同一条直线上,M、N分别为AB、BC的中点,且AB=30,BC=10,则MN的长是 .17. 下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第个图形中面积为1的正方形有2024个.
16. 已知A、B、C三点在同一条直线上,M、N分别为AB、BC的中点,且AB=30,BC=10,则MN的长是 .17. 下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第个图形中面积为1的正方形有2024个.
三、解答题
-
18. 计算:(1)、;(2)、 .19. 解方程:(1)、2x+3=﹣3x﹣7;(2)、 .20. 已知|x+2|+(y-3)2=0,先化简,再求值:21. 有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
﹣3
﹣2
﹣1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)、20筐白菜中,最重的一筐比最轻的一筐多重多少千克?(2)、与标准重量比较,20筐白菜总计超过或不足多少千克?(3)、若白菜每千克售价2元,则出售这20筐白菜可卖多少元?22. 某超市计划购进甲、乙两种型号的节能灯共1000只,这两种节能灯的进价、售价如下表:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、如果进货款恰好为37000元,那么可以购进甲型节能灯多少只?(2)、超市为庆祝元旦进行大促销活动,决定对乙型节能灯进行打折销售,要求全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?23. 综合与实践:A、B、C三点在数轴上的位置如图所示,点C表示的数为6,BC=4,AB=12. (1)、数轴上点A表示的数为 , 点B表示的数为;(2)、动点P,Q同时从A,C出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动.点Q以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒;
(1)、数轴上点A表示的数为 , 点B表示的数为;(2)、动点P,Q同时从A,C出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动.点Q以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒;①求数轴上点P,Q表示的数(用含t的式子表示);
②t为何值时,P,Q两点重合;
③请直接写出t为何值时,P,Q两点相距5个单位长度.
24. 综合与探究已知∠AOB、∠BOC,∠AOB=90°,
 (1)、若∠BOC为锐角,OE、OD分别平分∠AOB和∠BOC,
(1)、若∠BOC为锐角,OE、OD分别平分∠AOB和∠BOC,①如图1,当射线OC在∠AOB外部,∠BOC=40°时,求∠EOD的度数;
②当∠BOC=α()时,则∠EOD的度数是 ▲ ;
(2)、若∠AOC和∠BOC均为小于平角的角,OE、OD分别平分∠AOC和∠BOC,①当∠BOC=40°,OC位置如图2所示时,求∠EOD的度数.
②当∠BOC=α时(0°<α<180°),则∠EOD的度数是 ▲ .