黑龙江省齐齐哈尔市富裕县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. 等于( )A、 B、 C、3 D、-32. 下列计算正确的是( )A、 B、 C、 D、3. 有下列四种说法:①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角,那么它们相等;④锐角和钝角互补.其中正确的是( )A、①② B、①③ C、①②③ D、①②③④4. 若单项式xm+5y2﹣n与4xyn是同类项,则m﹣2n的值是( )A、4 B、﹣6 C、8 D、﹣95. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
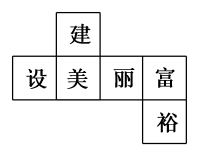 A、美 B、丽 C、富 D、裕6. 下列关于整式的说法中,正确的个数是( )
A、美 B、丽 C、富 D、裕6. 下列关于整式的说法中,正确的个数是( )①的系数是-3;② 4a3b的次数是3;③x2-1是二次二项式;④的各项分别为2a,b,1
A、1个 B、2个 C、3个 D、4个7. 方程与方程的解相同,则代数式的值为( )A、 B、 C、 D、8. 某商场在一次买卖中,同时卖出两件上衣,每件都以150元出售,若按成本计算,其中一件赢利50%,另一件亏本25%,在这次买卖中,该商场( )A、不盈不亏 B、盈利20元 C、亏损10元 D、盈利50元9. 将一副直角三角尺按如图所示的不同方式摆放,则图中与一定相等的是( )A、 B、
B、 C、
C、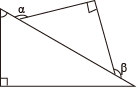 D、
D、 10. A、B两地相距350千米,甲、乙两车分别从A、B两地同时出发,相向而行,已知甲车速度为60千米/时,乙车速度为40千米/时,经过t小时两车相距50千米,则t的值是( )A、3.5 B、3.5或2.5 C、4 D、3或4
10. A、B两地相距350千米,甲、乙两车分别从A、B两地同时出发,相向而行,已知甲车速度为60千米/时,乙车速度为40千米/时,经过t小时两车相距50千米,则t的值是( )A、3.5 B、3.5或2.5 C、4 D、3或4二、填空题
-
11. 我国最新研制出的“曙光 超级服务器”的峰值速度达到 次/秒,数据 用科学记数法表示为.12. 已知方程(m﹣1)x|m|=6是关于x的一元一次方程,则m的值是13. 若 , 则= .14. 已知:数a,b,c在数轴上的对应点如图所示,化简|b﹣a|+|b﹣c|= .
 15. 若多项式与多项式的和是三次三项式,则的值为 .16. 点C是线段AB的中点,点D是线段AC的三等分点,若线段AB=18cm,则线段BD的长为 .17. 小王利用计算机设计了一个计算程序,输入和输出的数据如下表:那么,当输入数据为10时,输出的数据为 .
15. 若多项式与多项式的和是三次三项式,则的值为 .16. 点C是线段AB的中点,点D是线段AC的三等分点,若线段AB=18cm,则线段BD的长为 .17. 小王利用计算机设计了一个计算程序,输入和输出的数据如下表:那么,当输入数据为10时,输出的数据为 .输入
…
1
2
3
4
5
…
输出
…
…
三、解答题
-
18. 计算(1)、(2)、(3)、19. 计算(1)、计算:(2)、先化简,再求值:若 , 求多项式的值.20. 解方程(1)、(2)、-=121. 一个角的余角比它的补角的 还少50°,求这个角的度数.22. 如图,B,C两点把线段AD分成2∶5∶3三部分,M为AD的中点,BM=15 ,求CM和AD的长.
 23. 为抗击新冠肺炎疫情,某药店对消毒液和口罩开展优惠活动.消毒液每瓶定价10元,口罩每包定价5元,优惠方案有以下两种:①以定价购买时,买一瓶消毒液送一包口罩;②消毒液和口罩都按定价的80%付款.现某客户要到该药店购买消毒液30瓶,口罩包().(1)、若该客户按方案①购买需付款元(用含的式子表示);若该客户按方案②购买需付款元(用含的式子表示);(2)、试求当取何值时,方案①和方案②的购买费用一样;(3)、若时,按方案购买较为省钱.24. 直角三角板的直角顶点在直线上,平分 .
23. 为抗击新冠肺炎疫情,某药店对消毒液和口罩开展优惠活动.消毒液每瓶定价10元,口罩每包定价5元,优惠方案有以下两种:①以定价购买时,买一瓶消毒液送一包口罩;②消毒液和口罩都按定价的80%付款.现某客户要到该药店购买消毒液30瓶,口罩包().(1)、若该客户按方案①购买需付款元(用含的式子表示);若该客户按方案②购买需付款元(用含的式子表示);(2)、试求当取何值时,方案①和方案②的购买费用一样;(3)、若时,按方案购买较为省钱.24. 直角三角板的直角顶点在直线上,平分 . (1)、在图1中,若 , 求;(2)、在图1中,若 , (用含的式子表示);(3)、将图1中的三角板绕顶点旋转至图2的位置,探究:写出和的度数之间的关系,并说明理由.
(1)、在图1中,若 , 求;(2)、在图1中,若 , (用含的式子表示);(3)、将图1中的三角板绕顶点旋转至图2的位置,探究:写出和的度数之间的关系,并说明理由.