黑龙江省牡丹江市林口县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 2020年我国武汉暴发新冠肺炎疫情，全国人民发扬“一方有难.八方支援”的精神，积极参与到武汉防疫抗疫保卫战中.据统计，参与到武汉防疫抗疫中的全国医护人员约为42000人，将42000这个数用科学记数法表示正确的是（）

A、 $42 \times 10^{3}$ B、 $4.2 \times 10^{4}$ C、 $0.42 \times 10^{5}$ D、 $4.2 \times 10^{3}$

查看试题解析
2. 下列各式结果是负数的是（　　）

A、﹣（﹣3） B、﹣|﹣3| C、+|﹣3| D、（﹣3）²

查看试题解析
3. 下列各式计算正确的是（）
①0.667≈0.7（精确到十分位）
②|-3|-（-4）=-1
③2m+3m=5m
④38.15°=38°9′

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析
4. 下列各组两项中，是同类项的是（）

A、 $x y$ 与 $- x y$ B、 $\frac{1}{5} a b c$ 与 $\frac{1}{5} a c$ C、 $- 2 x y$ 与 $- 3 a b$ D、 $3 x^{2} y$ 与 $3 x y^{2}$

查看试题解析
5. 如图是一个数值转换机，例如输入a＝5，第一步5²＝25，第二步25﹣4×5＝5，第三步5×（﹣3），输出结果为﹣15．若输入a＝﹣5，则输出结果应为（）

A、15 B、135 C、-135 D、15

查看试题解析
6. 如图，点C、D在线段AB上，D是线段AB的中点，AC= $\frac{1}{3}$ AD，CD=4cm，则线段AB的长为（）

A、12 B、14 C、16 D、18

查看试题解析
7. 下面的图形中是正方体的展开图的是（）

A、 B、 C、 D、

查看试题解析
8. 将一副直角三角尺如图放置，若 $∠ A O D = 25 °$ ，则 $∠ B O C$ 的大小为（）

A、165° B、155° C、145° D、160°

查看试题解析
9. 某商贩在一次买卖中，同时卖出两件上衣，每件都以80元出售，若按成本计算，其中一件赢利60%，另一件亏本20%，在这次买卖中，该商贩（）

A、不盈不亏 B、盈利10元 C、亏损10元 D、盈利50元

查看试题解析
10. 已知等式 $3 a = 2 b + 5$ ，则下列等式中不一定成立的是（）

A、 $3 a - 5 = 2 b$ B、 $3 a + 1 = 2 b + 6$ C、 $3 a c = 2 b c + 5$ D、 $a = \frac{2}{3} b + \frac{5}{3}$

查看试题解析
11. 如图所示，甲从A点出发向北偏东60°方向走到点B，乙从点A出发向南偏西20°方向走到点C，则∠BAC的度数是（）.

A、80° B、100° C、120° D、140°

查看试题解析
12. 下列说法：①射线AB和射线BA是同－条射线；②锐角和钝角互补；③若一个角是钝角，则它的一半是锐角；④一个锐角的补角比这个角的余角大90度．⑤若线段AC=BC，则C是线段AB的中点；其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 比较大小：﹣ $\frac{2}{3}$ ﹣ $\frac{2}{5}$ ．

查看试题解析
14. 若 $| a + 3 | + {(b - 2)}^{2} = 0$ ，则 ${(a + b)}^{2021} =$ ．

查看试题解析
15. 下列叙述中，正确的有（填序号）．
①单项式5×10³x²y的次数是3；
②x﹣2xy+y是一次三项式；
③ $3 x - \frac{1}{x} = 1$ 是一元一次方程；
④如果 $\frac{a}{c} = \frac{b}{c}$ ，那么 $a = b$ ；
⑤两个数相加，它们的和一定大于其中一个数；
⑥互为相反数的两个数的绝对值相等．

查看试题解析
16. 关于x的一元一次方程 $2 {x^{a}}^{﹣ 2} + m ＝ 4$ 的解为x＝1，则a+m的值为．

查看试题解析
17. 如图所示，在一条笔直公路 p 的两侧，分别有甲、乙两个村庄，现要在公路 p 上建一个汽车站，使汽车站到甲、乙两村的距离之和最小，你认为汽车站应该建在处(填A 或 B 或 C)，理由是.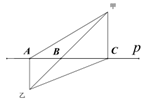

查看试题解析
18. 如图，A，O，B三点在一条直线上，∠AOC＝3∠COD，OE平分∠BOD，∠COE＝80°，则∠COD的度数是．

查看试题解析
19. 数轴上点 $A$ 和点 $B$ 表示的数分别是 $- 1$ 和3，点 $P$ 到 $A$ 、 $B$ 两点的距离之和为6，则点 $P$ 表示的数是 .

查看试题解析
20.
如图，这是由边长为1的等边三角形摆出的一系列图形，按这种方式摆下去，则第n个图形的周长是．

查看试题解析

三、解答题

21.

(1)、计算： $- 3^{2} + (- 2)^{2} \times (- 5) - | - 6 |$ ；

(2)、解方程： $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$ ；

(3)、先化简，再求值： $(3 a b^{2} - a^{2} b) - 2 (2 a b^{2} - a^{2} b)$ ，其中 $a = 1 ， b = - 2$ ．

查看试题解析
22. 若点C在射线AB上，若AB＝3，BC＝2，则AC为多少？请画出图形，并在相应的图形下直接写出答案．

查看试题解析
23. 有理数a、b、c在数轴上的位置如图：

(1)、用“＞”或“＜”填空a0，b0，c﹣b0，ab0．

(2)、化简：|a|+|b+c|﹣|c﹣a|．

查看试题解析
24. 已知点B在线段AC上，点D在线段AB上．

(1)、如图1，若AB=6cm，BC=4cm，D为线段AC的中点，求线段DB的长度；

(2)、如图2，若BD= $\frac{1}{4}$ AB= $\frac{1}{3}$ CD，E为线段AB的中点，EC=12cm，求线段AC的长度．

查看试题解析
25. 点O为直线AB上一点，将一直角三角板OMN的直角顶点放在点O处．射线OC平分∠MOB．

(1)、如图1，若∠AOM＝30°，求∠CON的度数；

(2)、在图1中，若∠AOM＝a，直接写出∠CON的度数（用含a的代数式表示）；

(3)、将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置，一边OM在射线OB上方，另一边ON在直线AB的下方．探究∠AOM和∠CON的度数之间的关系，写出你的结论，并说明理由．

查看试题解析
26. 某校计划购买20张书柜和一批书架（书架不少于20只），现从A、B两家超市了解到：同型号的产品价格相同，书柜每张210元，书架每只70元，A超市的优惠政策为每买一张书柜赠送一只书架，B超市的优惠政策为所有商品八折，设购买书架a只．

(1)、若该校到同一家超市选购所有商品，则到A超市要准备元货款，到B超市要准备元货款（用含a的式子表示）；

(2)、在（1）的情况下，当购买多少只书架时，无论到哪一家超市所付货款都一样？

(3)、假如你是本次购买的负责人，学校想购买20张书柜和100只书架，且可到两家超市自由选购，请你设计一种购买方案，使付款额最少，最少付款额是多少？

查看试题解析