黑龙江省鸡西市密山市2021-2022学年七年级上学期期末数学试题
试卷更新日期：2022-09-30 类型：期末考试
一、单选题
-
1. 如果水位下降3m记作－3m，那么水位上升5m记作（ ）A、1m B、3m C、+5m D、－5m2. 下列方程为一元一次方程的是（ ）A、y+3=0 B、x+2y=3 C、x2=2x D、+y=23. 下列各组数中，互为相反数的是（ ）A、-（-1）与1 B、（-1）2与1 C、 与1 D、-12与14. 下列各组单项式中，为同类项的是（ ）A、a3与a2 B、 a2与2a2 C、2xy与2x D、－3与a5. 下列各图中，可以是一个正方体的平面展开图的是（ ）A、
B、
C、
D、
6. 火星和地球的距离约为34 000 000千米，用科学记数法表示34 000 000的结果是（ ）千米．A、0.34×108 B、3.4×106 C、34×106 D、3.4×1077. 把两块三角板按如图所示那样拼在一起，则∠ABC等于（ ）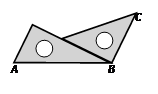
A、70° B、90° C、105° D、120°8. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（ ）
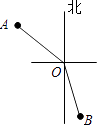A、69° B、111° C、141° D、159°9. 一件夹克衫先按成本提高50%标价，再以8折（标价的80%）出售，结果获利28元，若设这件夹克衫的成本是x元，根据题意，可得到的方程是（ ）A、（1＋50%）x×80%＝x－28 B、（1＋50%）x×80%＝x＋28 C、（1＋50%x）×80%＝x－28 D、（1＋50%x）×80%＝x＋2810. 轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/时，水速为2千米/时，求A港和B港相距多少千米．设A港和B港相距x千米．根据题意，可列出的方程是（ ）A、 B、 C、 D、二、填空题
-
11. 一个角的余角为50°，则这个角的补角等于 ．12. 数轴上点A表示的数是﹣4，点B表示的数是3，那么AB= ．13. 已知线段AB=8cm，在直线AB上画线段BC，使它等于3cm，则线段AC=cm．14. 若三角形的三边长分别是3a，2a-b，a+2b，则三角形的周长是 ．15. 若x=2是方程8﹣2x=ax的解，则a=16. 计算：15°37′+42°51′=17. 一个热气球在200米的空中停留，然后它依次上升了15米，﹣8米，﹣20米，这个热气球此时停留在米．18. 已知，a－b=2，那么2a－2b+5= ．19. 计算： ，则 = ．20. 现定义某种运算“*”，对给定的两个有理数a、b（a≠0），有a*b=ab，（-4）*2=
三、解答题
-
21. 计算(1)、－3＋10－9-10．(2)、(3)、（-3）3－︱－4＋（－3）2︱×（－2）322. 解方程(1)、7x+2（3x-3）=20(2)、23. 化简求值（5a－3b）－3（a－2b） 其中a=3 ，b=224. 如图，∠AOB＝∠COD＝90°，OC平分∠AOB，∠BOD＝3∠DOE.试求∠COE的度数.
