黑龙江省哈尔滨市木兰县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是( )A、-5x-1 B、5x+1 C、-13x-1 D、13x+14. 下列等式变形正确的是( )A、如果a=b , 那么a+c=b﹣c B、如果a2=5a , 那么a=5 C、如果a=b , 那么 D、如果 ,那么a=b5. 若是方程的解,则( )A、 B、 C、 D、6. 下列语句正确的是( )A、延长线段到 , 使 B、反向延长线段 , 得到射线 C、取射线的中点 D、连接A、B两点,使线段过点7. 是北偏东30°方向的一条射线,是北偏西50°方向的一条射线,那么的大小为( )A、 B、 C、 D、8. 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
 A、b>a B、ab>0 C、b-a>0 D、a+b>09. 欣欣服装店某天用相同的价格120元卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈亏情况是( )A、亏损10元 B、盈利10元 C、不盈不亏 D、盈利20元10. 分别从正面、左面和上面三个方向看下面哪个几何体,能得到如图所示的平面图形( )
A、b>a B、ab>0 C、b-a>0 D、a+b>09. 欣欣服装店某天用相同的价格120元卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈亏情况是( )A、亏损10元 B、盈利10元 C、不盈不亏 D、盈利20元10. 分别从正面、左面和上面三个方向看下面哪个几何体,能得到如图所示的平面图形( ) A、
A、 B、
B、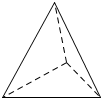 C、
C、 D、
D、
二、填空题
-
11. 中国的陆地面积约为9 600 000km2 , 把9 600 000用科学记数法表示为 .12. 比较大小:-- , (填“>”、“<”或“=”)13. 已知单项式与的和是单项式,则的值是 .14. 已知: , 则的值为.15. 若的补角是它的3倍,则的度数为.16. 如图: , , 射线OD平分 , 则 .
 17. 已知 , , 则 .18. 按如图所示的运算程序,输入 , , 则输出y的值是 .
17. 已知 , , 则 .18. 按如图所示的运算程序,输入 , , 则输出y的值是 . 19. 已知线段 , 直线AB上有一点C,且 , M是BC的中点,则AM的长是 .20. 如图1,小长方形纸片的长为2,宽为1,将4张这样的小长方形按图2所示的方式不重叠的放在长方形内,未被覆盖的部分恰好被分割为两个长方形A和B,设长方形A和B的周长分别为和 , 则(填“>”、“=”或“<”)
19. 已知线段 , 直线AB上有一点C,且 , M是BC的中点,则AM的长是 .20. 如图1,小长方形纸片的长为2,宽为1,将4张这样的小长方形按图2所示的方式不重叠的放在长方形内,未被覆盖的部分恰好被分割为两个长方形A和B,设长方形A和B的周长分别为和 , 则(填“>”、“=”或“<”)
三、解答题
-
21. 计算(1)、(2)、22. 先化简,再求值: ,其中 .23. 解方程(1)、(2)、24. 2020年为了应对武汉新冠肺炎疫情,需要快速建立医院,某车间连夜加班生产医用设备,现共有60个工人可以生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和每3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好都配套?25. 某校计划购买20张书柜和一批书架(书架不少于20只),现从A、B两家超市了解到:同型号的产品价格相同,书柜每张210元,书架每只70元,A超市的优惠政策为每买一张书柜赠送一只书架,B超市的优惠政策为所有商品八折,设购买书架a只.(1)、若该校到同一家超市选购所有商品,则到A超市要准备元货款,到B超市要准备元货款(用含a的式子表示);(2)、在(1)的情况下,当购买多少只书架时,无论到哪一家超市所付货款都一样?(3)、假如你是本次购买的负责人,学校想购买20张书柜和100只书架,且可到两家超市自由选购,请你设计一种购买方案,使付款额最少,最少付款额是多少?26. 如图1,线段AB长为24个单位长度,动点P从A出发,以每秒2个单位长度的速度沿射线AB运动,M为AP的中点,设P的运动时间为x秒.
 (1)、P在线段AB上运动,当时,求x的值.(2)、当P在线段AB上运动时,求的值.(3)、如图2,当P在AB延长线上运动时,N为BP的中点,MN的长度是否发生变化?如不变,求出MN的长度.如变化,请说明理由.27. 如图1,点在直线上, , 在中, , , 先将一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)、P在线段AB上运动,当时,求x的值.(2)、当P在线段AB上运动时,求的值.(3)、如图2,当P在AB延长线上运动时,N为BP的中点,MN的长度是否发生变化?如不变,求出MN的长度.如变化,请说明理由.27. 如图1,点在直线上, , 在中, , , 先将一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转. (1)、如图1,当OD在OA与OC之间,且时,则 .(2)、试探索:在的旋转过程中,与大小的差是发生变化?若不变,请求出这个差值,若变化,请说明理由.(3)、在的旋转过程中,若 , 试求的大小.
(1)、如图1,当OD在OA与OC之间,且时,则 .(2)、试探索:在的旋转过程中,与大小的差是发生变化?若不变,请求出这个差值,若变化,请说明理由.(3)、在的旋转过程中,若 , 试求的大小.