黑龙江省哈尔滨市巴彦县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、- $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列计算错误的是（）

A、 $3 a + 2 a = 5 a$ B、 $- b - b = - 2 b$ C、 $2 a^{2} b^{2} - 2 a b = a b$ D、 $5 a^{3} b - 3 b a^{3} = 2 a^{3} b$

查看试题解析
3. 下面四个几何体中，从正面看得到的图形是圆形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，线段AB的长为14cm，点C为线段AB的中点，点D在线段AC上， $A D = 5 c m$ ，则线段CD的长为（）

A、7cm B、5cm C、9cm D、2cm

查看试题解析
5. 小丽同学在做作业时，不小心将方程2（x－3）－■＝x＋1中的一个常数污染了，在询问老师后，老师告诉她方程的解是x＝9，请问这个被污染的常数■是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 某同学用剪刀沿直线将一片平整的荷叶剪掉一部分 $($ 如图 $)$ ，发现剩下的荷叶的周长比原银杏叶的周长要小，能符合题意解释这一现象的数学知识是 $($ $)$

A、经过两点有一条直线，并且只有一条直线 B、两条直线相交只有一个交点 C、两点之间所有连线中，线段最短 D、两点之间线段的长度，叫做这两点之间的距离

查看试题解析
7. 如图，甲从A处出发沿北偏东60°向走向B处，乙从A处出发沿南偏西30°方向走到C处，则∠BAC的度数是（）

A、 $16 0^{∘}$ B、 $15 0^{∘}$ C、 $12 0^{∘}$ D、 $9 0^{∘}$

查看试题解析
8. 李华和赵亮从相距30千米的A、B两地同时出发，李华每小时走4千米，3小时后两个人相遇，设赵亮的速度为 $x$ 千米/时，所列方程正确的是（）

A、 $3 (x + 4) = 30$ B、 $3 \times 4 + x = 30$ C、 $3 x + 4 = 30$ D、 $3 (x - 4) = 30$

查看试题解析
9. 如图，OP平分∠AOB，若图中所有小于平角的度数之和是192°，则∠AOP的度数是（）

A、91° B、64° C、48° D、32°

查看试题解析
10. 下列描述错误的是（）

A、单项式 $- \frac{a b^{2}}{3}$ 的系数是 $- \frac{1}{3}$ ，次数是3次； B、同角的余角相等； C、三棱锥有4个面，6条棱： D、-2000既是负数，也是整数，但不是有理数．

查看试题解析

二、填空题

11. 把数字3120000用科学记数法表示为．

查看试题解析
12. 已知∠α＝20′，∠β＝0.35°，则∠α∠β．（填“＞”，“＝”，或“＜”）

查看试题解析
13. 计算： $- {(\frac{2}{3})}^{2} + \frac{1}{9} =$ ．

查看试题解析
14. 已知 $∠ α = 67 °$ ，则∠α的补角为．

查看试题解析
15. 若 $2 (a + 3)$ 的值与-5的相反数相等，则a= ．

查看试题解析
16. 若a﹣b＝1，c+d＝﹣2，则（a+c）﹣（b﹣d）的值是 .

查看试题解析
17. 若 $- \frac{1}{2} x y^{n}$ 与 $2 x^{m} y^{3}$ 是同类项，则 $m - n =$ ．

查看试题解析
18. 如图，A、B、C、D依次是直线m上的四个点，且线段 $A B + C D = 5$ ，则线段 $A D - B C =$

查看试题解析
19. 已知 $∠ A O B = 20 °$ ， $∠ A O C = 70 °$ ， OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是．

查看试题解析
20. 如图，已知∠AOB＝150°，∠COD＝40°，∠COD在∠AOB的内部绕点O任意旋转，若OE平分∠AOC，则2∠BOE﹣∠BOD的值为°．

查看试题解析

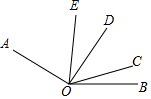
三、解答题

21.

(1)、计算： ${(- 2)}^{2} + | 5 - 8 | + 24 \div (- 3)$ ；

(2)、解方程： $\frac{x}{2} + \frac{x + 1}{3} = 1$ ．

查看试题解析
22. 如图，已知平面内四点A、B、C、D，根据下列条件画出图形：
（ 1 ）作射线AD；
（ 2 ）作直线BC与射线AD交于点P；
（ 3 ）连接AB．

查看试题解析
23. 先化简，再求值； $2 (x^{2} - 2 x) + (3 x^{2} + 5 x)$ ，其中 $x = - 2$ ．

查看试题解析
24. 如图1，OC是∠AOB的平分线，且 $∠ B O D = \frac{1}{3} ∠ C O D$ ．

(1)、当 $∠ B O D = 15 °$ 时，求∠AOB的度数：

(2)、如图2，若射线OP在 $∠ A O D$ 的内部，且 $∠ P O D = ∠ A O B$ ，请直接写出图中相等的四对角．（ $∠ P O D = ∠ A O B$ 和 $∠ B O C = ∠ A O C$ 除外）

查看试题解析
25. 某电器商场销售A、B两种型号计算器，两种计算器的进货价格分别为每台30元和40元，已知每台A型号的计算器的售价比每台B型号的计算器售价少14元，商场销售6台A型号和3台B型号计算器，可获利润120元；

(1)、求商场销售A种型号计算器的销售价格是多少元？

(2)、商场准备购进A、B两种型号计算器共70台，且所用资金为2500元，则需要购进B型号的计算器多少台？

查看试题解析
26. 如图， $∠ A O B = ∠ D O C = 90 °$ ．

(1)、试说明∠AOD与∠BOC互补；

(2)、如图2，当射线OA、OB都在∠COD的外部时，过点O作射线OE、OF，若射线OE是∠BOE的三等分线（ $∠ B O E < ∠ C O E$ ）， $∠ D O F = 2 ∠ A O F$ ，求 $∠ E O F$ 的度数：

(3)、如图3，在（2）的条件下， $∠ A O F = ∠ B O C + ∠ C O E$ ，射线OM平分∠EOD，过点O作射线ON，使 $∠ F O N ： ∠ F O M = 2 ： 5$ ，求 $∠ A O N$ 的度数．

查看试题解析
27. 如图，已知点O为数轴的原点，数轴上两点A、B，点A在原点的左侧，且 $O B = 3 O A$ ，点A表示的数的平方等于16．

(1)、请直接写出点A与点B表示的数；

(2)、点C为线段OB上一点，若 $A C = 3 (O C - B C)$ ，求点C表示的数；

(3)、在（2）的条件下，点M以2个单位/秒的速度从点A出发沿着数轴的正方向运动；同时点N以3个单位/秒的速度从点C出发，也沿着数轴的正方向运动，到达B点处立刻返回沿着数轴向终点A运动，直到点M到与点N相遇，点M停止运动，点N继续向点A运动，点P为AN的中点，点Q为MP的中点，设点N运动的时间为t，在此运动过程中，当M、N相遇后，t为何值时 $M N = \frac{12}{7} P Q$ ?

查看试题解析