广东省清远市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 如图是某几何体的展开图，该几何体是（）

A、长方体 B、圆柱 C、圆锥 D、三棱柱

查看试题解析
2. 分别由5个大小相同的正方体组成的甲、乙两个几何体，从同一个方向看到的几何体形状图完全一致的是（）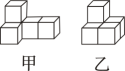

A、从正面看 B、从左面看 C、从上面看 D、以上都不对

查看试题解析
3. 下列说法正确的是（）

A、长方体的截面形状一定是长方形； B、棱柱侧面的形状可能是一个三角形； C、“天空划过一道流星”能说明“点动成线”； D、圆柱的截面一定是长方形．

查看试题解析
4. 2021年5月22日，我国自主研发的“祝融号”火星车成功到达火星表面．已知火星与地球的最近距离约为55000000千米，数据55000000用科学记数法表示为（）

A、55×10⁶ B、5.5×10⁷ C、5.5×10⁸ D、0.55×10⁸

查看试题解析
5. 小明做了以下 $3$ 道计算题：① $- 2 - 2 = 0$ ；② $- 2 - (- 2) = - 4$ ；③ $- 3 + 5 - 6 = - 4$ ，请你帮他检查一下，他一共做对了（）

A、 $1$ 道 B、 $2$ 道 C、 $3$ 道 D、 $0$ 道

查看试题解析
6. 一辆货车从超市出发，向东走了3km到达小彬家，继续向东走了1.5km到达小颖家，然后向西走了9.5km到达小明家，最后回到超市．小明家距小彬家（） km．

A、4.5 B、6.5 C、8 D、13.5

查看试题解析
7. 若2m﹣n﹣4＝0，则－2m＋n﹣9值是（）

A、－13 B、－5 C、5 D、13

查看试题解析
8. x＝3是下列方程中（）的解．

A、5（x－1）＝1 B、2－5（x－1）＝1 C、5（x－1）－3x＝1 D、5（x－1）＋8＝0

查看试题解析
9. 一个两位数，个位上的数字是a，十位上的数字是b，用代数式表示这个两位数是（）

A、ab B、ba C、10a+b D、10b+a

查看试题解析
10. 古希腊数学家把1，3，6，10，15，21，…叫做三角形数，其中1是第一个三角形数，3是第2个三角形数，6是第3个三角形数，…依此类推，那么第7个三角形数（）

A、25 B、27 C、28 D、33

查看试题解析

二、填空题

11. 计算：（－3）²＋6＝

查看试题解析
12. 比较有理数的大小： $| - 3 |$ －1（填＜、＝或＞）

查看试题解析
13. 如图，已知B是AC的中点，C是BD的中点，若BC＝2cm，则AD＝cm．

查看试题解析
14. 七（2）班第一组的12名同学身高（单位：cm）如下：162，157，161，164，154，153，156，168，153，152，165，158，那么身高在155～160的频数是．

查看试题解析
15. 把弯曲的河道改直，能够缩短航程，这样做根据的道理是 .

查看试题解析
16. 四名同学想了解所在城市的小学生是否感觉学习压力大，他们各自提出了自己的调查设想．
甲：周末去公园，随机询问10个小学生，就可以知道大致情况了．
乙：我有个弟弟，正在上小学，成绩中等，问问他就可以了解绝大部分学生的感受了．
丙：我妈妈是小学老师，向她询问就可以了．
丁：到不同的小学校门随机询问100个小学生，就可以了解大部分学生的感受了．
你觉得这四位同学提出的调查方式，能比较客观地反映“他们所在城市的小学生是否感觉学习压力大”是的调查方式．（填甲或乙或丙或丁）

查看试题解析
17. 观察下列等式：1＝1²﹣0² ， 3＝2²﹣1² ， 5＝3²﹣2² ， …按此规律，则第n个等式为．

查看试题解析

三、解答题

18. 计算：－2²÷2－3×（－11）

查看试题解析
19. 化简： $2 (m n + 3 m^{2}) - [2 m^{2} + 4 (m n + m^{2}) - 2 m n]$

查看试题解析
20. 如图，∠AOC和∠BOD都是直角．如果∠DOC＝28°，

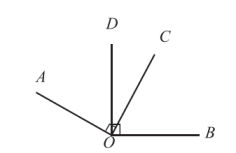(1)、求∠AOD 的度数；

(2)、求∠AOB的度数．

查看试题解析

21. 在创建“浙江省健康促进学校”的过程中，某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查，并按照国家分类标准统计人数，绘制成如下两幅不完整的统计图表，请根据图信息解答下列问题：

抽取的学生视力情况统计表

类别	检查结果	人数
A	正常	88
B	轻度近视
C	中度近视	59
D	重度近视

(1)、求所抽取的学生总人数；

(2)、该校共有学生约1800人，请估算该校学生中，近视程度为中度和重度的总人数；

(3)、请结合上述统计数据，为该校做好近视防控，促进学生健康发展提出一条合理的建议．

查看试题解析

22. 某中学开学初到商场购买A．B两种品牌的额温枪，购买A种品牌的额温枪50个，B种品牌的额温枪25个，共花费4500元，已知购买一个B种品牌的额温枪比购买两个A种品牌的额温枪少花20元．

(1)、如果购买一个A种品牌的额温枪a元，则购买一个B种品牌额温枪元（用含a的式了表示）．

(2)、求购买一个A种品牌的额温枪和一个B种品牌的额温枪各需多少元；

(3)、由于疫情比预计的时间要长，学校决定第二次购买A、B两种品牌额温枪共50个．正好赶上商场对商品价格进行调整，A种品牌额温枪售价比第一次购买时提高了8%，B种品牌额温枪按第一次购买时售价的九折出售．如果学校第二次购买A、B两种品牌额温枪的总费用是第一次购买额温枪总费用的70%，求学校第二次购买A种品牌的额温枪多少个．

查看试题解析
23. 对于任意有理数a和b，我们规定：a*b＝a²﹣2ab，如1*2＝1²﹣2×1×2＝﹣3

(1)、求6*7的值；

(2)、若（﹣3）*（2x）＝21，求x的值．

查看试题解析
24. 用边长为10cm的正方形纸按右图方式剪去四个边长相等的小正方形制作无盖长方体形盒子．

(1)、如果剪去的小正方形边长按0.5cm的间隔取值依次变化，即分别取0.5cm，1cm，1.5cm，2cm，2.5cm，3cm，3.5cm，4cm，4.5cm时，折成的无盖长方体形盒子的容积分别是多少？请你将计算的结果填入下表，并制作折线统计图．
剪去小正方形的边长/cm
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
容积/cm³
40.5
64
72
62.5
31.5
16
4.5
0

(2)、观察统计图，当小正方形边长变化时，所得到的无盖长方体形盒子的容积是如何变化的？

(3)、观察统计图，当小正方形边长取什么值时，所得到的无盖长方体形盒子的容积最大？此时，无盖长方体形盒子的容积是多少？

查看试题解析
25. 如图所示，在数轴上点A，B，C表示得数为﹣2，0，6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC．

(1)、求AB、AC的长；

(2)、点A，B，C开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和4个单位长度的速度向右运动．请问：BC﹣AB的值是否随着运动时间t的变化而变化？若不变，请求其值；若变化，请说明理由并判断是否有最值，若有求其最值．

查看试题解析

剪去小正方形的边长/cm	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5
容积/cm³	40.5	64		72	62.5		31.5	16	4.5	0