广东省梅州市平远县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列几何体，都是由平面围成的是（）

A、圆柱 B、三棱柱 C、圆锥 D、球

查看试题解析
2. 在－2，－3，0，2四个数中，最小的一个是（）

A、0 B、2 C、－2 D、－3

查看试题解析
3. 已知下列方程：①x﹣2＝ $\frac{1}{x}$ ；②0.4x＝1；③ $\frac{1}{x}$ ＝2x﹣2；④x﹣y＝6；⑤x＝0.其中一元一次方程有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 据猫眼实时数据显示，电影《长津湖》在上映第12天，累计票房正式突破4020000000元，这一数字用科学记数法表示为（）

A、 $40.2 \times 1 0^{8}$ B、 $4.02 \times 1 0^{9}$ C、 $40.2 \times 1 0^{9}$ D、 $4.02 \times 1 0^{10}$

查看试题解析
5. 某校在八年级成立了书法、绘画、体育、歌舞手工五个兴趣小组，每位学生只能参加一个兴趣小组，学生会对学生参加情况进行了问卷调查，并初步绘制了扇形统计图（如图），但图中未显示歌舞和手工部分，请你根据图中信息判断参加歌舞兴趣小组的学生人数一定不可能是（）

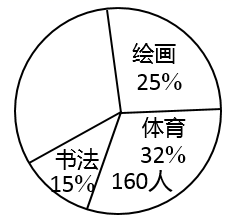A、50人 B、100人 C、130人 D、200人

查看试题解析
6. 从n边形的一个顶点出发，可以作5条对角线，则n的值是（）

A、6 B、8 C、10 D、12

查看试题解析
7. 若x＝﹣1是关于x的方程2x+m＝1的解，则m+1的值是（）

A、4 B、2 C、﹣2 D、﹣1

查看试题解析
8. 学校新建教学大楼拟用不锈钢制造一个上部是一个长方形、下部是一个正方形的窗户，相关数据(单位米)如图所示，那么制造这个窗户所需不锈钢的总长是（）

A、(4a+2b)米 B、(a²+ab)米 C、(6a+2b)米 D、(5a+2b)米

查看试题解析
9. 一个几何体是由一些大小相同的小正方体摆成其主视图和左视图如图所示则组成这个几何体的小正方体最少有 $a$ 个，最多有 $b$ 个， $b - a =$ （）

A、3 B、4 C、5 D、6

查看试题解析
10. 如图所示的运算程序中，若开始输入的x值为24，我们发现第1次输出的结果为12，第2次输出的结果为6，…，则第2021次输出的结果为（）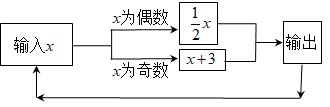

A、6 B、3 C、24 D、12

查看试题解析

二、填空题

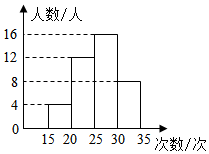
11. 用一个平面去截长方体，三棱柱，圆柱，和圆锥，其中不能截出三角形的几何体是.

查看试题解析
12. － $(- 1)^{2022}$ 的相反数是．

查看试题解析
13. 若单项式 $- \frac{1}{3} x^{2 m - 3} y^{4}$ 与3x⁵yn⁺¹的和仍是单项式，则mn＝．

查看试题解析
14. 为了解某校九年级学生的体能情况，学校随机抽查了其中的40名学生，测试了一分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，则仰卧起坐的次数在20～30之间的频数是．

查看试题解析
15. 如图，在直线l上依次有A、B，C三点，则图中线段共有条，射线共有条。

查看试题解析
16. 在等式 $3 a + 5 = 2 a + 6$ 的两边同时减去一个多项式可以得到等式 $a = 1$ ，则这个多项式是．

查看试题解析
17. 定义：对任意有理数 $a$ ， $b$ 都有 $a ∇ b = - a - b^{2}$ ，例如： $2 ∇ 1 = - 2 - 1^{2} = - 3$ ，求 $(2027 ∇ 1) ∇ 3 =$ .

查看试题解析

三、解答题

18. 计算： $(- 2)^{3} \times (- \frac{3}{4}) + 30 \div (- 5) - | - 3 |$ ．

查看试题解析
19. 在如图所示的六个方格中，分别填入-2；4； $- \frac{1}{2}$ ；8； $\frac{1}{4}$ ； $\frac{1}{8}$ ，使围成正方体后相对两面的两个数互为倒数．

查看试题解析
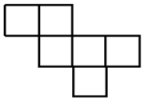20. 先化简，再求值： $3 (a^{2} - 2 a b) - [a^{2} - 3 b + 3 (a b + b)]$ ，其中 $a = - 3$ ， $b = \frac{1}{3}$ ．

查看试题解析
21. 为传承中华优秀传统文化，提升学生文学素养，某中学开展“假期读一本好书”的活动．某校为了了解学生活动开展的情况，从全校学生中随机抽取了部分学生调查他们的读书种类情况，并进行统计分析，绘制了不完整的统计图表．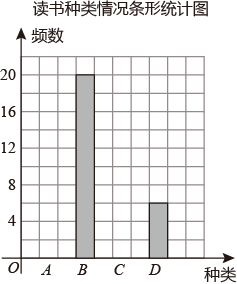
种类
频数
占抽取总人数的百分比
A．科普类
a
32%
B．文学类
20
b
C．艺术类
8
c
D．其他类
6
12%
请根据以上信息解答下列问题：

(1)、求统计表中a，b，c的值；

(2)、补全条形统计图；

(3)、若绘制“读书种类情况扇形统计图”，求“文学类”所对应扇形的圆心角度数．

查看试题解析
22. 已知有理数ab＜0，a+b＞0，且|a|=2，|b|=3．

(1)、求a、b的值；

(2)、求 $| a - \frac{2}{3} | \div 2 b$ 的值．

查看试题解析
23. 某商场从厂家购进了甲、乙两种商品，甲种商品的每件进价比乙种商品的每件进价少20元．若购进甲种商品7件，乙种商品2件，需要760元．

(1)、求甲、乙两种商品的每件进价分别是多少元？

(2)、该商场从厂家购进了甲、乙两种商品共50件，所用资金恰好为4400元．在销售时，甲种商品的每件售价为100元，要使得这50件商品卖出后获利20%，乙商品的每件售价为多少元？

查看试题解析
24. 如图①，点O为直线AB上一点，过点O作射线OC，使∠AOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．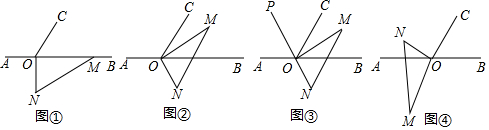

(1)、将图①中的三角板OMN摆放成如图②所示的位置，使一边OM在∠BOC的内部，当OM平分∠BOC时，求∠BON的度数；

(2)、在（1）的条件下，作线段NO的延长线OP（如图③所示），试说明射线OP是∠AOC的平分线；

(3)、将图①中的三角板OMN摆放成如图④所示的位置，请探究∠NOC与∠AOM之间的数量关系，并说明理由．

查看试题解析
25. 如图，在数轴上有A、B两点，点C是线段AB的中点，AB=12，OA=8．

(1)、求点C所表示的数；

(2)、动点P、Q分别从A、B同时出发，沿着数轴的正方向运动，点P、Q的运动速度分别是每秒3个单位和每秒2个单位（当P与Q相遇，运动停止），点M是线段PQ的中点，设运动时间为t秒，请用含t的式子表示CM的长；

(3)、在（2）的条件下，试问t为何值时，CM= $\frac{5}{2}$ PC

查看试题解析

种类	频数	占抽取总人数的百分比
A．科普类	a	32%
B．文学类	20	b
C．艺术类	8	c
D．其他类	6	12%