广东省惠州市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-30 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. “全民行动,共同节约”,我国14亿人口如果都响应国家号召每人每年节约1度电,一年可节 约1 400 000 000度电,这个数用科学记数法表示,正确的是( )A、1.40×108 B、1.4×109 C、0.14×1010 D、1.4×10103. 当A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,记作( )A、海拔23米 B、海拔﹣23米 C、海拔175米 D、海拔129米4. 下列平面图形经过折叠不能围成正方体的是( )A、
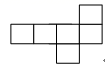 B、
B、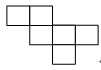 C、
C、 D、
D、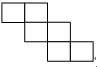 5. 下列关于单项式 的说法中,正确的是( )A、系数是2,次数是2 B、系数是 ,次数是3 C、系数是 ,次数是2 D、系数是 ,次数是36. 如图,甲、乙两人同时从A 地出发,甲沿北偏东50° 方向步行前进,乙沿图示方向步行前进.当甲到达B 地,乙到达C 地时,甲与乙前进方向的夹角∠BAC 为100° ,则此时乙位于A地的( )
5. 下列关于单项式 的说法中,正确的是( )A、系数是2,次数是2 B、系数是 ,次数是3 C、系数是 ,次数是2 D、系数是 ,次数是36. 如图,甲、乙两人同时从A 地出发,甲沿北偏东50° 方向步行前进,乙沿图示方向步行前进.当甲到达B 地,乙到达C 地时,甲与乙前进方向的夹角∠BAC 为100° ,则此时乙位于A地的( ) A、南偏东30° B、南偏东50° C、北偏西30° D、北偏西50°7. 下列计算中正确的是( )A、5a+6b=11ab B、9a﹣a=8 C、a2+3a=4a3 D、3ab+4ab=7ab8. 下列解方程的步骤中正确的是( )A、由x-5=7,可得x-7=5 B、由8-2(3x+1)=x,可得8-6x-2=x C、由 , 可得 D、由 , 可得9. “喜茶”店中的A种奶茶比B种奶茶每杯贵5元 ,小颖买了3杯A种奶茶、5杯B种奶茶,一共花了135元,问A种奶茶、B种奶茶每杯分别的多少元?若设A种奶茶 元,则下列方程中正确的是( )A、 B、 C、 D、10. 下列一组数:1,2,3,4,3,2,1,2,3,4,3,2,1,2,…其中第2022个数是( )A、1 B、2 C、3 D、4
A、南偏东30° B、南偏东50° C、北偏西30° D、北偏西50°7. 下列计算中正确的是( )A、5a+6b=11ab B、9a﹣a=8 C、a2+3a=4a3 D、3ab+4ab=7ab8. 下列解方程的步骤中正确的是( )A、由x-5=7,可得x-7=5 B、由8-2(3x+1)=x,可得8-6x-2=x C、由 , 可得 D、由 , 可得9. “喜茶”店中的A种奶茶比B种奶茶每杯贵5元 ,小颖买了3杯A种奶茶、5杯B种奶茶,一共花了135元,问A种奶茶、B种奶茶每杯分别的多少元?若设A种奶茶 元,则下列方程中正确的是( )A、 B、 C、 D、10. 下列一组数:1,2,3,4,3,2,1,2,3,4,3,2,1,2,…其中第2022个数是( )A、1 B、2 C、3 D、4二、填空题
-
11. 填空:1.4142135≈(精确到0.001)12. 若∠α= , 则∠α的余角度数是 .13. 若 +(b﹣3)2=0,则ab= .14. 若(k-2)x|k|-1=6是关于x的一元一次方程,则k的值为 .15. 如图所示是一个运算程序,若输出的结果是-2,则输入的值为 .
 16. 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑥个图形中实心圆点的个数为;
16. 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑥个图形中实心圆点的个数为; 17. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的有(填序号)
17. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的有(填序号)①b+c>0;②a+b>a+c;③bc<ac;④ab>ac.
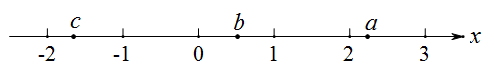
三、解答题
-
18. 计算:19. 解方程:20. 如图,∠AOB=120°,OC、OE、OF是∠AOB内的三条射线,且∠COE=60°,OF平分∠AOE,∠COF=20°,求∠BOE的度数.
 21. 先化简,再求值: , 其中x是最大的负整数,y是3的倒数.22. 定义一种新运算“⊕”,其运算规则为:a⊕b=-2a+3b,如:1⊕5=(-2)×1+3×5=13.在以上运算规则下,解决下列问题.(1)、计算:2⊕(-3)(2)、解方程:x⊕2=1023. 某超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
21. 先化简,再求值: , 其中x是最大的负整数,y是3的倒数.22. 定义一种新运算“⊕”,其运算规则为:a⊕b=-2a+3b,如:1⊕5=(-2)×1+3×5=13.在以上运算规则下,解决下列问题.(1)、计算:2⊕(-3)(2)、解方程:x⊕2=1023. 某超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)、该商场购进甲、乙两种商品各多少件?(2)、该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?24. 阅读材料:我们知道,4x-2x+x=(4-2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)、把(a−b)2看成一个整体,合并3(a−b)2−6(a−b)2+2(a−b)2的结果是.(2)、已知=4,求−21的值;(3)、已知a−2b=3,2b−c=−5,c−d=10,求(a−c)+(2b−d)−(2b−c)的值.25. 如图,在数轴上点A表示的数为﹣30,点B表示的数为80.动点C从点A出发以每秒6个单位的速度沿正方向运动,动点D从原点出发以每秒4个单位的速度沿正方向运动,动点E从点B出发以每秒8个单位的速度先沿负方向运动,到达原点后立即按原速返回,三点同时出发,设运动的时间为t(单位:秒). (1)、当t=7秒时,C、D、E三点在数轴上所表示的数分别为 , , ;(2)、当点D与点E的距离为56个单位时,求t的值;(3)、若点E回到点B时,三点停止运动,在三个动点运动过程中,是否存在某一时刻,这三点中有一点(除点D外)恰好在另外两点之间,且与两点的距离相等?若存在,请求出t的值;若不存在,请说明理由.
(1)、当t=7秒时,C、D、E三点在数轴上所表示的数分别为 , , ;(2)、当点D与点E的距离为56个单位时,求t的值;(3)、若点E回到点B时,三点停止运动,在三个动点运动过程中,是否存在某一时刻,这三点中有一点(除点D外)恰好在另外两点之间,且与两点的距离相等?若存在,请求出t的值;若不存在,请说明理由.