广东省河源市江东新区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中不是正方体的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
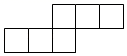2. 下列各式中，正确的是（）

A、 $- 4 - 2 = - 2$ B、 $3 - (- 3) = 0$ C、 $10 + (- 8) = - 2$ D、 $- 5 - 4 - (- 4) = - 5$

查看试题解析
3. 下列计算正确的是（）

A、 $3 (a + b) = 3 a + b$ B、 $- a^{2} b + b a^{2} = 0$ C、 $x^{2} + 2 x^{2} = 3 x^{4}$ D、 $2 m + 3 n = 5 m n$

查看试题解析
4. 将一副三角板按如图所示的方式放置，则 $∠ A O B$ 的大小为(　　)

A、 $80 °$ B、 $75 °$ C、 $60 °$ D、 $45 °$

查看试题解析
5. 已知 $x = 1$ 是关于x的一元一次方程 $2 x - a = 0$ 的解，则a的值为（）

A、 $- 1$ B、 $- 2$ C、1 D、2

查看试题解析
6. 西夏啤酒厂即将出厂一批啤酒，共装50辆汽车，每辆汽车装120箱，每箱24瓶．为了检测这批啤酒的合格率，现采用抽样抽查的方式，下列选取的样本，你认为最合理的是（）

A、选取一辆汽车全部检测 B、选取一辆汽车的一箱啤酒检测 C、选取一辆汽车的一箱啤酒中的2瓶进行检测 D、选取五辆汽车，每辆汽车中选取五箱，每箱选取2瓶进行检测

查看试题解析
7.
如图，C、D是线段AB上的两点，且D是线段AC的中点．若AB=10cm，BC=4cm，则AD的长为（　　）

A、2cm B、3cm C、4cm D、6cm

查看试题解析
8. 如图，把一张长方形纸片沿对角线 $B D$ 折叠， $∠ C B D = 25 °$ ，则 $∠ A B F$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
9. 某服装商贩同时卖出两套服装，每套均卖 $168$ 元，按成本计算，其中一套盈利 $20 %$ ，另一套亏本 $20 %$ ，则该商贩在这次经营中（）

A、亏本 $14$ 元 B、盈利 $14$ 元 C、不亏不盈 D、盈利 $20$ 元

查看试题解析
10. 如图所示的运算程序中，如果开始输入的 $x$ 值为 $- 48$ ，我们发现第1次输出的结果为 $- 24$ ，第2次输出的结果为 $- 12$ ， …，第2021次输出的结果为（）

A、 $- 6$ B、 $- 3$ C、 $- 24$ D、 $- 12$

查看试题解析

二、填空题

11. 下午 $3 ： 30$ 时，时钟上分针与时针的夹角是度．

查看试题解析
12. 如图，点 $A$ ， $B$ 在线段 $M N$ 上，则图中共有条线段.

查看试题解析
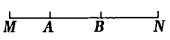13. 如果一个 $n$ 边形过一个顶点有 $8$ 条对角线，那么 $n =$ .

查看试题解析
14. 如果关于 $x$ 的方程 $x = 2 x - 3$ 和 $4 x - 2 m = 3 x + 2$ 的解相同，那么 $m =$ ．

查看试题解析
15. 某校共有 $2200$ 名学生，为了解学生对“七步洗手法”的掌握情况，随机抽取 $300$ 名学生进行调查，样本容量是．

查看试题解析
16. $A$ ， $B$ 两地相距 $450$ 千米，甲、乙两车分别从 $A$ ， $B$ 两地同时出发，相向而行，已知甲速度为 $120$ 千米/时，乙速度为 $80$ 千米/时， $t$ 小时后两车相距 $50$ 千米， $t$ 满足的方程是.

查看试题解析
17. 按一定规律排列的单项式：a，﹣2a，4a，﹣8a，16a，﹣32a，64a，…，第2021个单项式是．

查看试题解析

三、解答题

18. 计算：

(1)、 $4 \times (- 2) + (- 3) \div (- \frac{3}{5})$ ；

(2)、 $(- 1)^{2} + 12 \times (\frac{1}{4} - \frac{1}{6})$ ．

查看试题解析
19. 解方程 $\frac{1 - x}{4} + 1 = \frac{2 x + 1}{3}$ ．

查看试题解析
20. 先化简，再求值： $\frac{2}{3} (6 m - 9 m n) - (n^{2} - 6 m n)$ ，其中 $m = 1$ ， $n = - 3$ .

查看试题解析
21. 某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图：
根据图中提供的信息，解答下列问题：

(1)、 $m =$ ， E组对应的圆心角度数为 $°$ ；

(2)、补全频数分布直方图；

查看试题解析
22. 如图，已知直线 $A E ， O$ 是直线 $A E$ 上一点． $O B$ 是 $∠ A O C$ 的平分线， $O D$ 是 $∠ C O E$ 的平分线． $∠ A O B = 30 °$

(1)、求 $∠ C O E$ 的度数；

(2)、求 $∠ B O D$ 的度数．

查看试题解析
23. 在五一期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话(如图)，试根据图中的信息，解答下列问题：

(1)、小明他们一共去了几个成人，几个学生？

(2)、请你帮助小明算一算，用哪种方式购票更省钱？并说明理由.

查看试题解析
24. 已知数轴上有 $A ， B$ 两点，分别代表 $- 40 ， 20$ ，两只电子蚂蚁甲，乙分别从 $A ， B$ 两点同时出发，甲沿线段 $A B$ 以1个单位长度/秒的速度向右运动，甲到达点B处时运动停止，乙沿 $B A$ 方向以4个单位长度/秒的速度向左运动．

(1)、甲，乙在数轴上的哪个点相遇？

(2)、多少秒时，甲、乙相距10个单位长度？

(3)、若乙到达A点后立刻掉头并保持速度不变，则甲到达B点前，甲，乙还能在数轴上相遇吗？若能，求出相遇点所对应的数：若不能，请说明理由．

查看试题解析
25. 观察下列各式：
$1^{3} + 2^{3} = 1 + 8 = 9$ ，而 $(1 + 2)^{2} = 9 ， ∴ 1^{3} + 2^{3} = (1 + 2)^{2}$ ；

$1^{3} + 2^{3} + 3^{3} = 36$ ，而 $(1 + 2 + 3)^{2} = 36 ， ∴ 1^{3} + 2^{3} + 3^{3} = (1 + 2 + 3)^{2}$ ；

$1^{3} + 2^{3} + 3^{3} + 4^{3} = 100$ ，而 $(1 + 2 + 3 + 4)^{2} = 100 ， ∴ 1^{3} + 2^{3} + 3^{3} + 4^{3} = (1 + 2 + 3 + 4)^{2}$ ；

(1)、猜想并填空：
$1^{3} + 2^{3} + 3^{3} + 4^{3} + 5^{3} =$ $^{2} =$ ；

(2)、根据以上规律填空：
$1^{3} + 2^{3} + 3^{3} + ⋯ + n^{3} =$ $^{2} =$ ；

(3)、求解： $1 6^{3} + 1 7^{3} + 1 8^{3} + 1 9^{3} + 2 0^{3}$ ．

查看试题解析