云南省玉溪市峨山彝族自治县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-29 类型:期末考试
一、单选题
-
1. 2021年12月3日,全长1035公里、总投资约50 500 000 000元的中老铁路全线开通运营,它是以中方为主投资建设、全线采用中国技术标准、使用中国设备并与中国铁路网直接连通的国际铁路.数据50 500 000 000用科学记数法可表示为( )A、0.505×1011 B、505×108 C、5.05×1010 D、50.5×1092. 如图,该几何体从正面看到的平面图形是( )
 A、
A、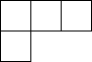 B、
B、 C、
C、 D、
D、 3. 下列计算错误的是( )A、 B、 C、 D、4. 已知x=﹣2是方程x+4a=10的解,则a的值是( )A、3 B、 C、2 D、﹣35. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
3. 下列计算错误的是( )A、 B、 C、 D、4. 已知x=﹣2是方程x+4a=10的解,则a的值是( )A、3 B、 C、2 D、﹣35. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、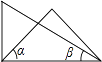 C、
C、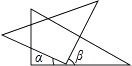 D、
D、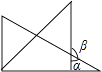 6. 有理数a,b在数轴上的位置如图所示,下列各式成立的是( )
6. 有理数a,b在数轴上的位置如图所示,下列各式成立的是( ) A、b>0 B、|a|>-b C、a+b>0 D、ab<07. 某校手工社团30名学生制作纸飞机模型,每人每小时可做20个机身或60个机翼,一个飞机模型要一个机身配两个机翼,为了使每小时制作的成品刚好配套,应该分配多少名学生做机身,多少名学生做机翼?设分配x名学生做机身,则可列方程为( )A、 B、 C、 D、8. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第n个图形中共有( )个“o”.
A、b>0 B、|a|>-b C、a+b>0 D、ab<07. 某校手工社团30名学生制作纸飞机模型,每人每小时可做20个机身或60个机翼,一个飞机模型要一个机身配两个机翼,为了使每小时制作的成品刚好配套,应该分配多少名学生做机身,多少名学生做机翼?设分配x名学生做机身,则可列方程为( )A、 B、 C、 D、8. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第n个图形中共有( )个“o”. A、3n B、3n+1 C、3n-1 D、3n+2
A、3n B、3n+1 C、3n-1 D、3n+2二、填空题
-
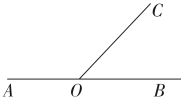
9. ﹣2的倒数是 .10. 若与是同类项,则m+n= .11. 如图,O是直线AB上一点,若∠BOC=60°,则∠AOC的度数为 .
 12. 已知式子的值是-2,则式子= .13. 当x=时,代数式6x+1与﹣2x﹣5的值互为相反数.14. 已知点C、点D在直线AB上,且AC=BD=1,若AB=7,则CD的长为 .
12. 已知式子的值是-2,则式子= .13. 当x=时,代数式6x+1与﹣2x﹣5的值互为相反数.14. 已知点C、点D在直线AB上,且AC=BD=1,若AB=7,则CD的长为 .三、解答题
-
15. 计算:16. 解方程:17. 先化简,再求值:
,其中 , .
18. 如图,C、D是线段AB上的两点,CB=5cm,DB=8cm,且点D是AC的中点,求线段DC和AB的长度. 19. 为了改善青少年体质健康状况,云南省中考改革把体育与语、数、英并列,按100分计入升学成绩,让体育从边缘化回归教育主阵地.为此,小健同学天天坚持跑步锻炼,他每天以1000米为标准,超过记为正数,不足记为负数,下表记录了小健同学上周的跑步情况:
19. 为了改善青少年体质健康状况,云南省中考改革把体育与语、数、英并列,按100分计入升学成绩,让体育从边缘化回归教育主阵地.为此,小健同学天天坚持跑步锻炼,他每天以1000米为标准,超过记为正数,不足记为负数,下表记录了小健同学上周的跑步情况:星期
一
二
三
四
五
六
日
跑步情况
+140
+120
﹣65
﹣100
+80
+125
+200
(1)、上周,小健同学跑步最多的一天比跑步最少的一天多跑了多少米?(2)、若小健同学跑步的平均速度为250米/分钟,则上周他累计用了多少分钟跑步?20. 如图,∠AOB=90°,OE平分∠AOB,OD平分∠BOC,∠EOD=70°,求∠BOC的度数.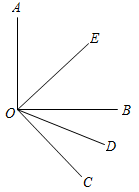 21. 为庆祝“建党100周年”,某学校组织“学党史”知识竞赛,共设20道选择题,每题必答,答对1题得5分,答错1题扣1分,参赛者小红得88分,则她答对几道题?22. 如今,网上购物已成为一种新的消费时尚,晶晶文具店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网店(如图所示),已知两家网店的这种贺年卡完全相同,根据图回答下列问题:
21. 为庆祝“建党100周年”,某学校组织“学党史”知识竞赛,共设20道选择题,每题必答,答对1题得5分,答错1题扣1分,参赛者小红得88分,则她答对几道题?22. 如今,网上购物已成为一种新的消费时尚,晶晶文具店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网店(如图所示),已知两家网店的这种贺年卡完全相同,根据图回答下列问题: (1)、若晶晶文具店想购买x张贺年卡,
(1)、若晶晶文具店想购买x张贺年卡,当时,在甲网店需要花费元,在乙网店需要花费元;
当时,在甲网店需要花费元,在乙网店需要花费元;
(提示:以上费用均用含x的式子表示,如需付运费时,运费只需付一次,即10元)
(2)、晶晶文具店打算购买200张贺年卡,选择哪家网店更省钱?23. 【阅读】在数轴上,点A对应的有理数为a,点B对应的有理数为b,则以A、B为端点的线段的长度AB= , 以A、B为端点线段的中点对应数为 .【运用】如图,已知A、B、C 分别为数轴上的两点,点A对应的数为-8,点B对应的数为 4,点C对应的数为6,现有一动点P从点A出发,以每秒3个单位长度的速度沿数轴向右运动;同时,另一动点Q从点B出发,以每秒5个单位长度的速度沿数轴向左运动,设运动时间为t秒.
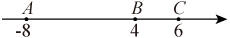 (1)、A,B两点间的距离AB= , 线段AB的中点表示的数为;(2)、用含t 的代数式表示:点P对应的数是 , 点Q对应的是 , 动点Q经过秒时运动到点A与点B的中点处;(3)、经过多少秒时,点P与点Q之间的距离恰好是点Q与点C之间距离的一半?
(1)、A,B两点间的距离AB= , 线段AB的中点表示的数为;(2)、用含t 的代数式表示:点P对应的数是 , 点Q对应的是 , 动点Q经过秒时运动到点A与点B的中点处;(3)、经过多少秒时,点P与点Q之间的距离恰好是点Q与点C之间距离的一半?