云南省昆明市嵩明县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-29 类型:期末考试
一、单选题
-
1. -2022的相反数是( )A、-2022 B、 C、2022 D、2. 探索浩瀚宇宙是全人类的共同梦想,2020年我们行驶在浩瀚的星辰大海,嫦娥五号克服种种困难,顺利完成月球采样,时隔四十多年再创人类“挖土”壮举,华盛顿大学空间科学中心主任提到这些样本有助于填补大约30亿年前至10亿年前月球历史知识的空白.嫦娥五号满载而归映照中国科技自立自强的铿锵步伐,也激励着人类共同探.索宇宙奥秘.30亿用科学记数法表示为( )A、 B、 C、 D、3. 如右图的几何体,从上面看,得到的平面图是( )
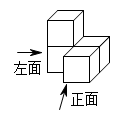 A、
A、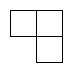 B、
B、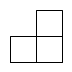 C、
C、 D、
D、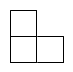 4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法错误的是( )A、是方程的解 B、和不是同类项 C、3.14是单项式 D、的系数是6. 鸿星尔克某件商品的成本价为a元,按成本价提高10%后标价,又以八折销售,这件商品的售价( )A、比成本价低了0.12a元 B、比成本价低了0.08a元 C、比成本价高了0.1a元 D、与成本价相同7. 如图,将一副三角尺按不同位置摆放,哪种摆放方式中与相等( )A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法错误的是( )A、是方程的解 B、和不是同类项 C、3.14是单项式 D、的系数是6. 鸿星尔克某件商品的成本价为a元,按成本价提高10%后标价,又以八折销售,这件商品的售价( )A、比成本价低了0.12a元 B、比成本价低了0.08a元 C、比成本价高了0.1a元 D、与成本价相同7. 如图,将一副三角尺按不同位置摆放,哪种摆放方式中与相等( )A、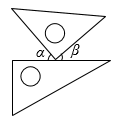 B、
B、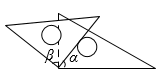 C、
C、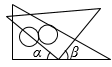 D、
D、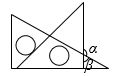 8. 将正方形做如下操作,第1次分别连接各边中点如图2,得到5个正方形;第2次将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2025个正方形,则需要操作的次数为( )
8. 将正方形做如下操作,第1次分别连接各边中点如图2,得到5个正方形;第2次将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2025个正方形,则需要操作的次数为( ) A、503 B、504 C、505 D、506
A、503 B、504 C、505 D、506二、填空题
-
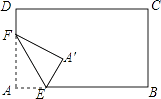
9. 从2021年3月份起,一共16头亚洲象离开了西双版纳自然保护区,开始踏上一路向北的旅程.如果大象向北走5km记作+5km,那么8km表示 .10. 若单项式3xym与-xny3是同类项,则m-n的值是.11. 计算: .12. 现用110立方米木料制作桌子和椅子,已知1张桌子配6把椅子,1立方米木料可做5把椅子或1张桌子.设用x立方米的木料做桌子,则依题意可列方程为 .13. 如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,则∠FEB的度数是 .
 14. 已知线段 , 点C在直线AB上,且 , 则线段BC的长为 .
14. 已知线段 , 点C在直线AB上,且 , 则线段BC的长为 .三、解答题
-
15. 按要求解答(1)、把下列各数填在相应的括号内:
, , , (每两个1之间逐次增加1个0), , , , ,
正有理数集合:{ …};
负数集合:{ …};
整数集合:{ …}.
(2)、画出数轴,并在数轴上表示下面5个原数,然后比较这5个原数的大小,用“<”号连接., , , ,
16. 计算:(1)、(2)、17. 解下列方程:(1)、(2)、18. 先化简,再求值:求代数式的值.其中 .19. 在庆祝新中国72周年华诞的重要时刻,电影《长津湖》上映可谓恰逢其时、意义重大.电影《长津湖》讲述了中国人民志愿军第9兵团某部穿插七连参加长津湖战役的过程,展现了人民军队炽烈的爱国情杯、对党和人民的无比忠诚,生动诠释了伟大的抗美援朝精神.昆明市9月30日该电影的售票量为1.3万张,10月1日到10月7日售票的变化如下表(正数表示售票量比前一天多,负数表示售票量比前一天少):日期
1日
2日
3日
4日
5日
6日
7日
售票量的变化单位(万张)
+0.6
+0.1
0.3
0.2
0.4
0.2
+0.1
(1)、这7天中,售票量最多的是10月日,售票量最少的是10月日;(2)、若平均每张票价为60元,这7天昆明市《长津湖》的票房共多少万元?20. 中老铁路是中国“一带一路”倡议重点项目之一,它的完工对倡议本身也有极其重大的意义,中老铁路已于2021年12月3日开通,列车开通后,给沿线的人民带来了极大的便利.小徐在A处上班,每周五去往B处回家看父母,坐高铁的时间比乘客车时间少30分钟,已知从A到B处坐高铁的路程比乘客车少20千米,若高铁行驶的平均速度为200千米/时,客车行驶的平均速度为100千米/时,求从A到B处乘客车的路程.21. 如图,已知点O为直线AB上的一点,OM平分 , , . (1)、求的度数;(2)、若与互余,求的度数.22. 近年来,国家越来越重视新能源汽车的发展,为积极响应国家推广节能减排的政策,李老师家买了一辆新能源汽车.现有两种充电方式,采用家用专用充电桩:每充一度电需付费0.6元,且需要花费2500元购买安装充电桩;采用公共充电桩充电:每充一度电需付费1.6元,不需要购买安装充电桩.(1)、若李老师家的车总计充电x度,请用含x的式子表示:采用家用专用充电桩充电的费用: , 采用公共充电桩充电的费用: .(2)、请你根据x的不同取值,为李老师设计一个省钱划算的方案.23. 如图,点A、B、C、O是在数轴上的点如图所示,其中点O表示的数是0,点A、B、C表示的数分别为a、b、c.
(1)、求的度数;(2)、若与互余,求的度数.22. 近年来,国家越来越重视新能源汽车的发展,为积极响应国家推广节能减排的政策,李老师家买了一辆新能源汽车.现有两种充电方式,采用家用专用充电桩:每充一度电需付费0.6元,且需要花费2500元购买安装充电桩;采用公共充电桩充电:每充一度电需付费1.6元,不需要购买安装充电桩.(1)、若李老师家的车总计充电x度,请用含x的式子表示:采用家用专用充电桩充电的费用: , 采用公共充电桩充电的费用: .(2)、请你根据x的不同取值,为李老师设计一个省钱划算的方案.23. 如图,点A、B、C、O是在数轴上的点如图所示,其中点O表示的数是0,点A、B、C表示的数分别为a、b、c.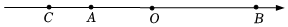 (1)、图中共有条线段.(2)、若 , O为CB的中点,且 , 求a、b、c的值.(3)、已知D为数轴上一点,当点D到点A的距离是点D到点B距离的4倍,则称点D是(A,B)的“四倍点”;当点D到点B的距离是点D到点A距离的4倍时,D是(B,A)的“四倍点”.若A、B表示的数为(2)中所求,且D在A的左边,是否存在使得A、B、D中恰有一个点是其余两个点的“四倍点”的情况.若存在,求出D表示的数;若不存在,请说明理由.
(1)、图中共有条线段.(2)、若 , O为CB的中点,且 , 求a、b、c的值.(3)、已知D为数轴上一点,当点D到点A的距离是点D到点B距离的4倍,则称点D是(A,B)的“四倍点”;当点D到点B的距离是点D到点A距离的4倍时,D是(B,A)的“四倍点”.若A、B表示的数为(2)中所求,且D在A的左边,是否存在使得A、B、D中恰有一个点是其余两个点的“四倍点”的情况.若存在,求出D表示的数;若不存在,请说明理由.