云南省昆明市盘龙区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. －2022的相反数是（）

A、－2022 B、 $\frac{1}{2022}$ C、2022 D、 $- \frac{1}{2022}$

查看试题解析
2. 截至2021年11月13日，全国累计报告我国3至11岁人群新冠疫苗接种超8400万人，力争年底完成该人群全程接种．数字84000000用科学记数法表示为（）

A、 $8.4 \times 1 0^{6}$ B、 $8.4 \times 1 0^{7}$ C、 $84 \times 1 0^{6}$ D、 $84 \times 1 0^{7}$

查看试题解析
3. 若 $∠ A = 48 ° 4 0^{'}$ ，则 $∠ A$ 补角的大小是（）

A、 $41 ° 2 0^{'}$ B、 $41 ° 6 0^{'}$ C、 $131 ° 2 0^{'}$ D、 $131 ° 6 0^{'}$

查看试题解析
4. 下列计算正确的是（）

A、3a²－a²=3 B、m＋n=2mn C、3x²＋x³=4x⁵ D、5x²y³－5y³x²=0

查看试题解析
5. 有三个正方体木块，每一块的各面都写上不同的数字，三块的写法完全相同，现把它们摆放成如图所示的位置请你判断数字5对面的数字是（）

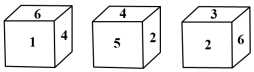A、6 B、3 C、2 D、1

查看试题解析
6. 一份数学试卷共25道选择题，每道题都给出了4个答案，其中只有一个符合题意选项，每道题选对得4分，不选或错选倒扣1分，已知小丽得了90分，设小丽做对了x道题，则下列所列方程正确的是（）

A、 $4 x - (25 - x) = 90$ B、 $x + 4 (25 - x) = 90$ C、 $4 x + (25 - x) = 90$ D、 $4 x - (25 + x) = 90$

查看试题解析
7. 如图是一个“数值转换机”，按下面的运算过程输入一个数x，若输入的数 $x = - 1$ ，则输出的结果为（）

A、15 B、13 C、11 D、 $- 5$

查看试题解析
8. 已知a、b、c在数轴上位置如图，则 $| a + b | + | a + c | - | c - b | =$ （）

A、 $0$ B、 $2 a + 2 b$ C、 $2 b - 2 c$ D、 $2 a + 2 c$

查看试题解析

二、填空题

9. 若 $x^{a + 3} y^{3}$ 与 $- \frac{1}{3} x y^{3}$ 是同类项，则a的值是．

查看试题解析
10. 关于x的一元一次方程2x﹣a＝3x+4解为x＝1，则a的值为．

查看试题解析
11. 已知 $a^{2} + 2 a = 8$ ，则 $2 a^{2} + 4 a - 5$ 的值为．

查看试题解析
12. 观察下列一组数： $\frac{2}{3} ， \frac{4}{5} ， \frac{6}{7} ， \frac{8}{9} ，$ $\frac{10}{11}$ ……它们是按一定规律排列的，那么这一组数的第k个数是．

查看试题解析
13. 已知∠AOB＝20°，∠AOC＝4∠AOB，OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是度

查看试题解析

三、解答题

14. 计算：

(1)、 $13 - 16 - 12 + 17$ ；

(2)、 $- 1^{2022} + (- 3)^{2} \div (\frac{1}{2} - \frac{1}{3}) - | - 8 |$ ．

查看试题解析
15. 计算与化简

(1)、7x²y﹣5xy﹣（4yx²﹣5xy）；

(2)、先化简，再求值：5（3m²n﹣mn²）﹣（mn²＋3m²n）＋2（﹣3m²n＋2mn²），其中，m＝﹣1，n＝2

查看试题解析
16. 解方程：

(1)、 $6 x - 2 = 5 x + 4$ ；

(2)、 $2 - \frac{2 x + 1}{3} = \frac{1 + x}{2}$ ．

查看试题解析

17. 某食堂购进30袋大米，每袋以50千克为标准，超过的记为正，不足的记为负，称重记录如下表．

与标准重量偏差（单位：千克）	$- 2$	$- 1$	0	1	2	3
袋数	5	10	3	1	5	6

(1)、这30袋大米的总重量比标准总重量是多还是少？相差多少？

(2)、大米单价是每千克5.5元，食堂购进大米总共花多少钱？

查看试题解析

18. 如图，已知DB＝2，AC＝10，点D为线段AC的中点，求线段BC的长度．

查看试题解析

19. 阅读下列材料，完成相应的任务：

对称式

一个含有多个字母的代数式中，如果任意交换两个字母的位置，代数式的值都不变，这样的代数式就叫做对称式．

例如：代数式 $a b c$ 中任意两个字母交换位置，可得到代数式 $b a c$ ， $a c b$ ， $c b a$ ，因为 $a b c = b a c = a c b = c b a$ ，所以 $a b c$ 是对称式；而代数式 $a - b$ 中字母a，b交换位置，得到代数式 $b - a$ ，因为 $a - b \neq b - a$ ，所以 $a - b$ 不是对称式．

任务：

(1)、下列四个代数式中，是对称式的是（填序号）；

① $a + b + c$ ；② $a + b$ ；③ $a b$ ；④ $\frac{a}{b}$ ．

(2)、写出一个只含有字母x，y的单项式，使该单项式是对称式，且次数为6；

(3)、已知

A = a^{2} b - 3 b^{2} a + \frac{4}{3} c^{2} a

，

B = a^{2} b - 5 b^{2} a + 2 c^{2} a

，求

3 A - 2 B

，并直接判断所得结果是否为对称式．

查看试题解析

20. 如图，直线 $A B$ 与直线 $C D$ 相交于点 $O$ ， $O E ⊥ A B$ ，垂足为 $O$ ， $∠ E O D = \frac{1}{2} ∠ A O C$ ，求 $∠ B O C$ 的度数．

查看试题解析
21. 为了美化环境，建设生态桂林，某社区需要进行绿化改造，现有甲、乙两个绿化工程队可供选择，已知甲队每天能完成的绿化改造面积比乙队多200平方米，甲队与乙队合作一天能完成800平方米的绿化改造面积.

(1)、甲、乙两工程队每天各能完成多少平方米的绿化改造面积？

(2)、该社区需要进行绿化改造的区域共有12000平方米，甲队每天的施工费用为600元，乙队每天的施工费用为400元，比较以下三种方案：①甲队单独完成；②乙队单独完成；③甲、乙两队全程合作完成.哪一种方案的施工费用最少？

查看试题解析
22. 数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合，研究数轴我们发现：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB＝|a﹣b|，线段AB的中点表示的数为 $\frac{a + b}{2}$ ．如：如图，数轴上点A表示的数为﹣2，点B表示的数为8，则A、两点间的距离AB＝|﹣2﹣8|＝10，线段AB的中点C表示的数为 $\frac{- 2 + 8}{2}$ ＝3，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动．设运动时间为t秒（t＞0）．

(1)、用含t的代数式表示：t秒后，点P表示的数为，点Q表示的数为．

(2)、求当t为何值时，P、Q两点相遇，并写出相遇点所表示的数；

(3)、求当t为何值时，PQ＝ $\frac{1}{2}$ AB；

(4)、若点M为PA的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．

查看试题解析