云南省德宏傣族景颇族自治州梁河县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. 如果收入200元记作+200元，那么支出150元记作（）

A、+150元 B、- 150元 C、+50元 D、-50元

查看试题解析
2. 下列方程中，是一元一次方程的是（）

A、 $\frac{1}{x} = - 1$ B、 $x^{2} = 4 x + 5$ C、 $8 - x = 1$ D、 $x + y = 7$

查看试题解析
3. 如图是从三个方向看某个几何体得出的平面图形，该几何体是（）

A、棱柱体 B、圆柱体 C、圆锥体 D、球体

查看试题解析
4. 数轴上A点表示﹣5，B点表示3，则AB之间有几个单位长度（　　）

A、﹣2 B、8 C、2 D、﹣8

查看试题解析
5. 若关于 $x ， y$ 的单项式 $- x^{m} y^{n - 1}$ 与 $5 x^{2} y^{3}$ 是同类项，则 ${(m - n)}^{3}$ 的值为（）

A、9 B、6 C、 $- 6$ D、 $- 8$

查看试题解析
6. 下列说法中正确的是（）

A、若 $| a | = - a$ ，则 $a$ 一定是负数 B、 $- 1$ 是最大的负整数 C、 $42 ° 3 9^{'} + 33 ° 3 1^{'} = 76 °$ D、若 $∠ A O C = \frac{1}{2} ∠ A O B$ ，则射线 $O C$ 是 $∠ A O B$ 的平分线

查看试题解析
7. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺．则正确的方程是（）

A、 $\frac{1}{2} x = (x - 5) - 5$ B、 $\frac{1}{2} x = (x + 5) + 5$ C、 $2 x = (x - 5) - 5$ D、 $2 x = (x + 5) + 5$

查看试题解析
8. 观察下列关于 $a$ 的单项式，探究其规律： $a ， 3 a^{2} ， 5 a^{3} ， 7 a^{4} ， 9 a^{5} ， ⋯$ ，按照上述规律，第2022个单项式是（）

A、 $2022 a^{2022}$ B、 $4045 a^{2022}$ C、 $4044 a^{2022}$ D、 $4043 a^{2022}$

查看试题解析

二、填空题

9. ﹣ $\frac{2}{3}$ 的倒数是．

查看试题解析
10. 单项式 $- \frac{a^{2} b^{3}}{3}$ 的系数是．

查看试题解析
11. 在墙壁上固定一根横放的木条，则至少需要2枚钉子，符合题意解释这一现象的数学知识是．

查看试题解析
12. 中华民族的母亲河黄河，发源于巴颜喀拉山脉北麓，注入渤海，流域面积约为 $750000 千米^{2}$ ，将 $750000 千米^{2}$ 用科学记数法表示为 $千米^{2}$ ．

查看试题解析
13. 若关于 $x$ 的方程 $2 x + 3 m - 1 = 0$ 和方程 $5 - 3 (x - 1) = 2$ 同解，则 $m$ 的值等于．

查看试题解析
14. 已知在同一平面内 $∠ A O B = 70 °$ 、 $∠ A O C = 45 °$ ，则 $∠ B O C =$ ．

查看试题解析

三、解答题

15. 计算：

(1)、 $14 - (- 16) + (- 10)$

(2)、 ${(- 1)}^{2021} - | - 8 | + {(- 3)}^{2} - (\frac{11}{8} - \frac{4}{3}) \times 24$

查看试题解析
16. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - 3 (a b^{2} + 5 a^{2} b)$ ，其中a＝3，b＝ $- \frac{1}{2}$ .

查看试题解析
17. 解方程：

(1)、 $3 x - 1 = 2 x + 3$

(2)、 $\frac{2 x - 1}{3} = 1 - \frac{x + 2}{4}$

查看试题解析
18. 一个角的补角等于它的余角的3倍，求这个角的度数．

查看试题解析
19. 如图， $C 、 D$ 是线段 $A B$ 上的两点，若 $C B = 5 c m$ ， $D B = 8 c m$ ，且 $D$ 是 $A C$ 的中点，求 $A B$ 的长．

查看试题解析
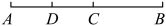20. 某口罩加工厂每名工人计划每天生产400个医用口罩，由于种种原因，实际每天生产量与计划量相比有出入．如下表是工人小王某周的生产情况（超产记为正，减产记为负）：
星期
一
二
三
四
五
六
日
增减产量/个
+5
-2
-4
+13
-9
+16
-8

(1)、根据记录的数据可知，小王星期五生产口罩多少个？

(2)、根据表格记录的数据，求出小王本周实际生产口罩数量．

查看试题解析
21. 如图，已知直线 $A B 、 C D$ 相交于点 $O$ ，射线 $O D$ 平分 $∠ B O F$ ， $O E ⊥ C D$ 于点 $O$ ， $∠ A O C = 35 °$ ．

(1)、求 $∠ E O F$ 的度数；

(2)、试判断射线 $O E$ 是否平分 $∠ A O F$ ，并说明理由．

查看试题解析
22. 某工厂生产茶具，每套茶具有1个茶壶和4只茶杯组成，生产这套茶具的主要材料是紫砂泥，用1千克紫砂泥可做2个茶壶或8只茶杯．现要用6千克紫砂泥制作这些茶具，应用多少千克紫砂泥做茶壶，多少个千克紫砂泥做茶杯，恰好配成这种茶具多少套？

查看试题解析
23. 目前节能灯已基本普及，某商场计划购进甲、乙两种节能灯共1200只，这两种节能灯的进价、售价如下表所示：

进价（元/只）
售价（元/只）
甲型
25
30
乙型
45
60

(1)、如何进货，进货款恰好为46000元？

(2)、如何进货，商场销售完节能灯时恰好获利30%，此时利润为多少元？

查看试题解析

星期	一	二	三	四	五	六	日
增减产量/个	+5	-2	-4	+13	-9	+16	-8

	进价（元/只）	售价（元/只）
甲型	25	30
乙型	45	60