安徽省合肥市肥西县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. 3的相反数为（）

A、 ﹣3 B、﹣ $\frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. “东风快递，使命必达”！东风-41是我国目前最先进的洲际战略导弹，假设其最快飞行速度是8500米/秒，则用科学记数法表示东风-41的最快飞行速度为（）

A、 $8.5 \times 1 0^{3}$ 米/秒 B、 $0.85 \times 1 0^{4}$ 米/秒 C、 $8.5 \times 1 0^{4}$ 米/秒 D、 $85 \times 1 0^{3}$ 米/秒

查看试题解析
3. 根据等式的性质，下列变形正确的是（）

A、由- $\frac{1}{3}$ x＝ $\frac{2}{3}$ y，得x＝2y B、由3x＝2x＋2，得x＝2 C、由2x－3＝3x，得x＝3 D、由3x－5＝7，得3x＝7－5

查看试题解析
4. 若 $x^{3} y^{a}$ 与 $x^{b} y$ 是同类项，则 $a + b$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 将大小相同的小圆按如图所示的规律摆放：第①个图形有5个小圆，第②个图形有10个小圆，第③个图形有17个小圆，…依此规律，第⑥个图形的小圆个数是（）

A、65 B、60 C、55 D、50

查看试题解析
6. 如图，OC是 $∠ A O B$ 的平分线，OD是 $∠ B O C$ 的平分线，那么下列各式中正确的是（）.

A、 $∠ C O D = \frac{1}{2} ∠ A O B$ B、 $∠ A O D = \frac{2}{3} ∠ A O B$ C、 $∠ B O D = \frac{1}{2} ∠ A O D$ D、 $∠ B O C = \frac{2}{3} ∠ A O D$

查看试题解析
7. 若 $| a | = 4$ ， $| b | = 2$ ，且 $a + b$ 的绝对值与它的相反数相等，则 $a + b$ 的值是（）

A、 $- 2$ B、 $- 6$ C、 $- 2$ 或 $- 6$ D、2或6

查看试题解析
8. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何？这道题的意思是：今有若干人乘车，每三人乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问有多少人，多少辆车？如果我们设有x辆车，则可列方程（）

A、3（x﹣2）＝2x＋9 B、3（x＋2）＝2x﹣9 C、 $\frac{x}{3}$ ＋2＝ $\frac{x - 9}{2}$ D、 $\frac{x}{3}$ ﹣2＝ $\frac{x + 9}{2}$

查看试题解析
9. 若 $∠ 1$ 与 $∠ 2$ 互为余角， $∠ 1$ 与 $∠ 3$ 互为补角，则下列结论：① $∠ 3 - ∠ 2 = 90 °$ ；② $∠ 3 + ∠ 2 = 270 ° - 2 ∠ 1$ ；③ $∠ 3 - ∠ 1 = 2 ∠ 2$ ；④ $∠ 3 < ∠ 1 + ∠ 2$ ．其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 若 $a$ 是最大的负整数， $b$ 是绝对值最小的有理数， $c$ 是倒数等于它本身的自然数，则 $a^{2021} + 2018 b + c^{2022}$ 的值为（）

A、2017 B、2018 C、2019 D、0

查看试题解析

二、填空题

11. 若 $x$ 是非负数，则 $x$ 0（填“>，≥，<，≤，=”中的一个）．

查看试题解析
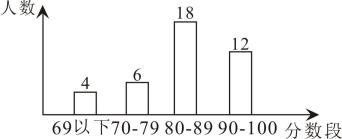
12. 如图是某班全班40名学生一次数学测验分数段统计图，根据统计图所提供的信息计算优良率（分数80分以上包括80分的为优良）为（填入百分数）．

查看试题解析
13. 为了解神舟飞船的设备零件的质量情况，选择抽样调查的方式是否合理（填是或否）．

查看试题解析
14. 如图，一个长方形的长为a，宽为b，将它剪去一个正方形①，然后从剩余的长方形中再剪去一个正方形③，最后剩下长方形②．请用含a、b的代数式表示：

(1)、正方形③的边长为．

(2)、长方形②的面积为．

查看试题解析
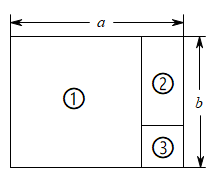15. 数轴上A，B两点分别为﹣10和90，两只蚂蚁分别从A，B两点出发，分别以每秒钟3个单位长和每秒钟2个单位长的速度匀速相向而行，经过秒，两只蚂蚁相距20个单位长．

查看试题解析

三、解答题

16.

(1)、 $- 1^{2022} + {(- 3)}^{2} \div (- \frac{9}{2}) + | - 3 - 2 | \times (1 - \frac{1}{5})$ ；

(2)、先化简，再求值： $3 m^{2} - [m n^{2} + 2 (\frac{3}{2} m^{2} - m n) + m n] + 3 m n^{2}$ ，其中 $m = - 4$ ， $n = 1$ ．

查看试题解析
17. 已知：如图，点 $C$ 是线段 $A B$ 的中点， $C D = 2 c m$ ， $B D = 8 c m$ ，求 $A D$ 的长．

查看试题解析
18. 如图，将两块直角三角尺的顶点叠放在一起．

(1)、若∠DCE＝35°，求∠ACB的度数；

(2)、若∠ACB＝140°，求∠DCE的度数；

(3)、猜想∠ACB与∠DCE的关系，并说明理由．

查看试题解析
19. 已知：如图①， $∠ A O B = 60 °$ ， $∠ C O D = 40 °$ ， $O B$ 与 $O C$ 重合， $O P$ 平分 $∠ A O C$ ， $O Q$ 平分 $∠ B O D$ ．

(1)、 $∠ P O Q =$

(2)、将 $∠ C O D$ 绕着点 $O$ 逆时针方向旋转，使 $∠ B O C = α (0 \leq α < 180 °)$ ，当 $α = 80 °$ 时，如图②，求 $∠ P O Q$ 的度数．

查看试题解析
20. 某中学七年级一班学生去商场购买了A品牌足球1个、B品牌足球2个，共花费210元，七年级二班同学在同一商场购买了A品牌足球3个、B品牌足球1个，共花费230元．

(1)、求A，B两种品牌足球的价格各为多少元？

(2)、为响应“足球进校园”的号召，学校使用专项经费1500元全部用来购买A，B两种品牌的足球供学生使用（要求两种足球都必须购买，专项经费必须用完），那么学校有多少种不同的购买方案？请分别求出每种方案购买A，B两种品牌足球的个数．

查看试题解析
21. 已知线段 $A B = 15 c m$ ，点 $C$ 在线段 $A B$ 上，且 $A C ： C B = 3 ： 2$ ．

(1)、求线段 $A C$ ， $C B$ 的长；

(2)、点 $P$ 是线段 $A B$ 上的动点且不与点 $A$ ， $B$ ， $C$ 重合，线段 $A P$ 的中点为 $M$ ，设 $A P = m c m$
①请用含有 $m$ 的代数式表示线段 $P C$ ， $M C$ 的长；
②若三个点 $M$ ， $P$ ， $C$ 中恰有一点是其它两点所连线段的中点，则称 $M$ ， $P$ ， $C$ 三点为“共谐点”，请直接写出使得 $M$ ， $P$ ， $C$ 三点为“共谐点”的 $m$ 的值．

查看试题解析