安徽省合肥市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-29 类型:期末考试
一、单选题
-
1. 下列各数中最小的是( )A、0.9 B、-3.6 C、-0.8 D、-(-2.5)2. 下面计算正确的是( )A、3x2-x2=3 B、3a2+2a3=5a5 C、3+x=3x D、﹣0.25ab+ ba=03. 已知下列方程:① ;② ;③ ;④ ;⑤ ;⑥ 其中一元一次方程的个数是( )A、2 B、3 C、4 D、54. 下列生活现象,可以用基本事实“两点之间,线段最短”解释的是( )A、汽车的雨刮器把玻璃上的水刷干净 B、开山挖隧道,把上坡下坡的盘山公路改为平直的隧道 C、公园的喷泉中,喷水龙头喷出的圆形水面 D、建筑工人通过在两个柱子之间拉一条绳子砌墙5. 为进一步巩固“双减”落实效果,了解某校七年级学生完成作业的时间情况,从中随机抽取了100名七年级学生进行调查,下列说法错误的是( )A、总体是某校七年级学生完成作业的时间 B、样本是抽取的100名七年级学生 C、个体是某校七年级每个学生完成作业的时间 D、样本容量是1006. 如图,已知线段AB=4 cm,延长AB至点C,使AC=11 cm.点D是AB的中点,点E是AC的中点,则DE的长为( )
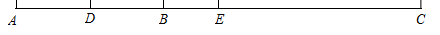 A、3 cm B、3.5 cm C、4 cm D、4.5 cm7. 若∠1与∠3互余,∠2与∠3互补,则∠1与∠2的关系是( )A、∠1=∠2 B、∠1与∠2互余 C、∠1与∠2互补 D、∠2-∠1=90°8. 已知|a|=3,|b|=4,且a>b,则ab的值为( )A、±1 B、±12 C、1或-7 D、7或-19. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )A、 B、 C、 D、10. 三张大小不一的正方形纸片按如图1和图2方式分别放置于相同的长方形中,它们既不重叠也无空隙,记图1阴影部分周长之和为m,图2阴影部分周长为n,要求m与n的差,只需知道一个图形的周长,这个图形是( )
A、3 cm B、3.5 cm C、4 cm D、4.5 cm7. 若∠1与∠3互余,∠2与∠3互补,则∠1与∠2的关系是( )A、∠1=∠2 B、∠1与∠2互余 C、∠1与∠2互补 D、∠2-∠1=90°8. 已知|a|=3,|b|=4,且a>b,则ab的值为( )A、±1 B、±12 C、1或-7 D、7或-19. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )A、 B、 C、 D、10. 三张大小不一的正方形纸片按如图1和图2方式分别放置于相同的长方形中,它们既不重叠也无空隙,记图1阴影部分周长之和为m,图2阴影部分周长为n,要求m与n的差,只需知道一个图形的周长,这个图形是( )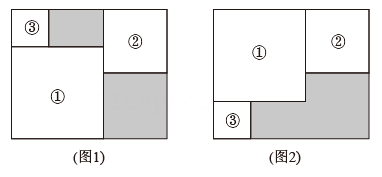 A、整个长方形 B、图①正方形 C、图②正方形 D、图③正方形
A、整个长方形 B、图①正方形 C、图②正方形 D、图③正方形二、填空题
-
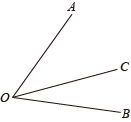
11. 若与是同类项,则k= .12. 如图,已知 , , 那么 . (用度、分、秒表示)
 13. 关于x,y的方程组的解的和为2,则a的值为 .14. 已知有理数a≠1,我们把称为a的差倒数.例如:2的差倒数是=-1,-1的差倒数是 . 如果 , 是的差倒数,是的差倒数……以此类推,那么的值是 .
13. 关于x,y的方程组的解的和为2,则a的值为 .14. 已知有理数a≠1,我们把称为a的差倒数.例如:2的差倒数是=-1,-1的差倒数是 . 如果 , 是的差倒数,是的差倒数……以此类推,那么的值是 .三、解答题
-
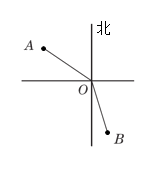
15. 计算: .16. 解方程(组):(1)、;(2)、 .17. 如图,在灯塔O处观测到轮船A位于北偏西56°的方向,轮船B位于南偏东17°的方向,求∠AOB的度数.
 18. 已知 ,求 的值.19. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,购买4千克的甲食材比购买5千克的乙食材多花60元.
18. 已知 ,求 的值.19. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,购买4千克的甲食材比购买5千克的乙食材多花60元.营养品信息表
营养成分
每千克含铁42毫克
配料表
原料
每千克含铁
甲食材
50毫克
乙食材
10毫克
(1)、甲、乙两种食材每千克的进价分别是多少元?(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完,那么该公司每日购进甲、乙两种食材各多少千克?20. 如图,点A在数轴上表示的数是-9,点D在数轴上表示的数是12,AB=4,CD=2. (1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长为;(2)、若点Q是数轴上的点,且QC=2QB,则点Q在数轴上表示的数是多少?21. 如图,将一个正方形纸片剪成四个正方形纸片,然后将其中的一个正方形纸片再剪成四个正方形纸片,再将其中的一个正方形纸片剪成四个正方形纸片,如此继续下去…,请你根据以上操作方法得到的正方形的个数的规律完成下列各题.
(1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长为;(2)、若点Q是数轴上的点,且QC=2QB,则点Q在数轴上表示的数是多少?21. 如图,将一个正方形纸片剪成四个正方形纸片,然后将其中的一个正方形纸片再剪成四个正方形纸片,再将其中的一个正方形纸片剪成四个正方形纸片,如此继续下去…,请你根据以上操作方法得到的正方形的个数的规律完成下列各题.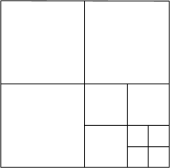 (1)、将下表填写完整.
(1)、将下表填写完整.操作次数
1
2
3
4
5
…
n
正方形的个数
4
7
10
…
(2)、= . (用含n的代数式表示)(3)、按照上述操作方法,能否得到2 022个正方形?如果能,请求出n;如果不能,请简述理由.22. 为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”“有害垃圾”“可回收物”和“其他垃圾”这四类标准将垃圾分类处理.调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制了如下不完整的统计图.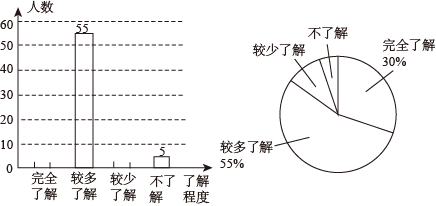 (1)、本次调查的样本容量是;(2)、补全条形统计图.23. 如图所示,O是直线上的一点,是直角,平分 .
(1)、本次调查的样本容量是;(2)、补全条形统计图.23. 如图所示,O是直线上的一点,是直角,平分 .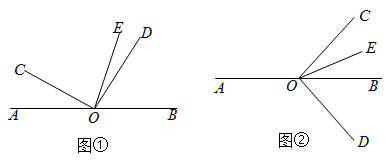 (1)、如图①,若 , 求的度数;(2)、在图①,若 , 直接写出的度数(用含a的代数式表示);(3)、将图①中的绕顶点O顺时针旋转至图②的位置.
(1)、如图①,若 , 求的度数;(2)、在图①,若 , 直接写出的度数(用含a的代数式表示);(3)、将图①中的绕顶点O顺时针旋转至图②的位置.①探究和的度数之间的关系,写出你的结论,并说明理由;
②在的内部有一条射线 , 满足 , 试确定与的度数之间的关系,说明理由.