安徽省滁州市定远县(藕塘片)2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-29 类型:期末考试
一、单选题
-
1. -2022的倒数是( )A、 B、 C、 D、2. 2021年12月23日,安徽省政府新闻办举办新闻发布会,就“皖北地区群众喝上引调水工程”的相关情况进行了介绍.其中,“皖北地区群众喝上引调水工程”规划布局供水工程76处,供水规模每天286万立方米,规划投资154亿元,将154亿用科学记数法表示为( )A、 B、 C、 D、3. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,两地间修建曲桥与修建直桥的桥对比,增加了桥的长度,其中蕴含的数学道理是( )
 A、两点之间,线段最短 B、过一点,有无数条直线 C、两点确定一条直线 D、连接两点之间线段的长度叫做两点间的距离4. 下列说法中,正确的是( )A、单项式与的和是多项式 B、的系数是1 C、用度表示是 D、一个锐角的补角一定大于它的余角5. 有理数a、b在数轴上的位置如图所示,则 ( )
A、两点之间,线段最短 B、过一点,有无数条直线 C、两点确定一条直线 D、连接两点之间线段的长度叫做两点间的距离4. 下列说法中,正确的是( )A、单项式与的和是多项式 B、的系数是1 C、用度表示是 D、一个锐角的补角一定大于它的余角5. 有理数a、b在数轴上的位置如图所示,则 ( )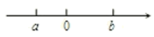 A、2a-2b B、-4b C、-2a-2b D、06. 如图,将一张长方形纸片分别沿着 , 折叠,使边 , 均落在上,得到折痕 , , 则等于( )
A、2a-2b B、-4b C、-2a-2b D、06. 如图,将一张长方形纸片分别沿着 , 折叠,使边 , 均落在上,得到折痕 , , 则等于( ) A、 B、 C、 D、7. 今年父亲的年龄是儿子的5倍,5年前父亲的年龄是儿子的15倍,设今年儿子的年龄为x,可得方程( )A、5x-5=15(x-5) B、5x+5=15(x-5) C、5x-5=15(x+5) D、5x+5=15(x+5)8. 学习了数据的收集、整理与表示之后,某小组同学对本校开设的 , , , , , 六门“自主选修活动课”的选课情况比较感兴趣,他们以问卷的形式随机调查了若干名学生的选课情况(每人只能选一门课),并将调查结果绘制成如下统计图(不完整):
A、 B、 C、 D、7. 今年父亲的年龄是儿子的5倍,5年前父亲的年龄是儿子的15倍,设今年儿子的年龄为x,可得方程( )A、5x-5=15(x-5) B、5x+5=15(x-5) C、5x-5=15(x+5) D、5x+5=15(x+5)8. 学习了数据的收集、整理与表示之后,某小组同学对本校开设的 , , , , , 六门“自主选修活动课”的选课情况比较感兴趣,他们以问卷的形式随机调查了若干名学生的选课情况(每人只能选一门课),并将调查结果绘制成如下统计图(不完整):选修课
人数
20
30

根据图表提供的信息,下列结论错误的是( )
A、这次被调查的学生人数为200人 B、被调查的学生中选课程的有55人 C、被调查的学生中选课程的人数为35人 D、被调查的学生中选课程的人数占20%9. 如图,点C是AB的中点,点D是BC的中点,则下列等式中成立的有( )①;②;③;④ .
 A、①② B、②③ C、①③ D、②④10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A、①② B、②③ C、①③ D、②④10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )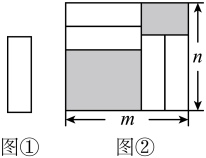 A、4m B、4n C、2(m+n) D、4(m-n)
A、4m B、4n C、2(m+n) D、4(m-n)二、填空题
-
11. -2.78 . (填“>”“<”或“=”)12. 一件羽绒服原价是元,后由于迎新年促销打折售价是元,这件羽绒服打了折.13. 已知是关于的方程的解,则的值是 .14. 如图,自行车每节链条的长度为 , 交叉重叠部分的圆的直径为 .

 (1)、4节链条拉直后长度为;(2)、n节链条拉直后长度为;(3)、如果一辆自行车的链条由50节这样的链条首尾环形相连组成,那么该自行车链条环的长度是 .
(1)、4节链条拉直后长度为;(2)、n节链条拉直后长度为;(3)、如果一辆自行车的链条由50节这样的链条首尾环形相连组成,那么该自行车链条环的长度是 .三、解答题
-
15. 已知点O为直线上一点,将直角三角板如图所示放置,且直角顶点在O处,在内部作射线 , 且恰好平分 .
 (1)、若 , 则=度;(2)、若 , 则=度.16. 计算: .17. 先化简,再求值:
(1)、若 , 则=度;(2)、若 , 则=度.16. 计算: .17. 先化简,再求值:, 其中a,b满足
18. 《九章算术》是中国古代《算经十书》最重要的一部,它的出现标志中国古代数学形成了完整的体系,其中有一道阐述“盈不足数”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?意思是说:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?19. 当今,人们对健康愈加重视,跑步成了人们进行体育锻炼的首要选择,许多与运动有关的手机 (即手机应用小程序)应运而生.小明爸爸给自己定了健身目标,每天跑步a千米.以目标路程为基准,超过的部分记为“+”,不足的部分记为“一”,他记下了“十一”长假期间七天跑步的实际路程如下:日期
1日
2日
3日
4日
5日
6日
7日
路程(千米)
(1)、10月5日小明爸爸的跑步路程是千米;(用含a的代数式表示)(2)、小明爸爸给自己定的健身目标是每天跑5千米,若跑步一千米消耗的热量为60千卡,求小明爸爸这七天跑步一共消耗了多少热量?20. 如图,点O是直线上的一点, , 平分 . (1)、试说明;(2)、求的度.21. 图①、图②反映是东方百货商场今年月份的商品销售额统计情况.来自商场财务部的报告表明,商场月份的销售总额一共是万元,观察图①和图②,解答下面问题:
(1)、试说明;(2)、求的度.21. 图①、图②反映是东方百货商场今年月份的商品销售额统计情况.来自商场财务部的报告表明,商场月份的销售总额一共是万元,观察图①和图②,解答下面问题:
 (1)、将图①补充完整;(2)、商场服装部5月份的销售额是多少万元?(3)、李强观察图②后认为,5月份服装部的销售额比4月份减少了.你同意他的看法吗?为什么?22. 某市有甲、乙两个工程队,现有-小区需要进行小区改造,甲工程队单独完成这项工程需要天,乙工程队单独完成这项工程所需的时间比甲工程队多 .(1)、求乙工程队单独完成这项工程需要多少天?(2)、现在若甲工程队先做5天,剩余部分再由甲、乙两工程队合作,还需要多少天才能完成?(3)、已知甲工程队每天施工费用为元,乙工程队每天施工费用为元,若该工程总费用政府拨款元(全部用完),则甲、乙两个工程队各需要施工多少天?23. 若数轴上点A,B所表示的数分别是a,b,则A,B两点之间的距离可表示为两点所表示的数的差的绝对值,即或 . 已知点A,B在数轴上,点A在数轴上对应的数为a,点B对应的数为b,且a,b满足 .(1)、求点A,B两点之间的距离;(2)、如果点P,Q分别同时从点A,B出发,沿数轴相向运动,点P每秒走1个单位长度,点Q每秒走2个单位长度,经过几秒P,Q两点相遇?此时点P,Q对应的数是多少?(3)、在(2)的条件下,整个运动过程中,设运动时间为t秒,点Q到达点A停止运动,若的中点为点M,的中点为点N,当t为何值时, .
(1)、将图①补充完整;(2)、商场服装部5月份的销售额是多少万元?(3)、李强观察图②后认为,5月份服装部的销售额比4月份减少了.你同意他的看法吗?为什么?22. 某市有甲、乙两个工程队,现有-小区需要进行小区改造,甲工程队单独完成这项工程需要天,乙工程队单独完成这项工程所需的时间比甲工程队多 .(1)、求乙工程队单独完成这项工程需要多少天?(2)、现在若甲工程队先做5天,剩余部分再由甲、乙两工程队合作,还需要多少天才能完成?(3)、已知甲工程队每天施工费用为元,乙工程队每天施工费用为元,若该工程总费用政府拨款元(全部用完),则甲、乙两个工程队各需要施工多少天?23. 若数轴上点A,B所表示的数分别是a,b,则A,B两点之间的距离可表示为两点所表示的数的差的绝对值,即或 . 已知点A,B在数轴上,点A在数轴上对应的数为a,点B对应的数为b,且a,b满足 .(1)、求点A,B两点之间的距离;(2)、如果点P,Q分别同时从点A,B出发,沿数轴相向运动,点P每秒走1个单位长度,点Q每秒走2个单位长度,经过几秒P,Q两点相遇?此时点P,Q对应的数是多少?(3)、在(2)的条件下,整个运动过程中,设运动时间为t秒,点Q到达点A停止运动,若的中点为点M,的中点为点N,当t为何值时, .