吉林省白城市通榆县2022-2023学年第一学期九年级数学第一次月考试题
试卷更新日期:2022-09-29 类型:月考试卷
一、单项选择题(每小题2分,共12分)
-
1. 一元二次方程x2+x-1=0的根的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、只有一个实数根2. 已知关于x的方程3x2-2x+m=0的一个根是1,则m的值为( )A、3 B、2 C、1 D、-13. 用配方法解方程x2-2x=2时,配方后正确的是( )A、(x+1)2=3 B、(x+1)2=6 C、(x-1)2=3 D、(x-1)2=64. 如表是代数式ax2+bx的值的情况,根据表格中的数据,可知方程ax2+bx=6的根是( )
x
……
-3
-2
-1
0
1
2
3
4
……
ax2+bx
……
12
6
2
0
0
2
6
12
……
A、x1=0,x2=1 B、x1=-1,x2=2 C、x1=-2,x2=3 D、x1=-3,x2=45. 把抛物线y=(x+1)2向下平移2个单位长度,再向右平移1个单位长度,所得到的抛物线是( )A、y=x2+2 B、y=x2-2 C、y=(x+2)2-2 D、y=(x+2)2+26. 已知二次函数y=-2x2+bx+c(其中b<0,c为常数),则该函数的图象可能为( )A、 B、
B、 C、
C、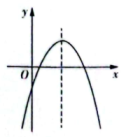 D、
D、
二、填空题(每小题3分,共24分)
-
7. 一元二次方程(x-1)(x+2)=0的根是8. 请填写一个常数,使得关于x的方程x2-2x+ =0有两个不相等的实数根.9. 有一个人患了流感,经过两轮传染后共有16个人患了流感,则每轮传染中平均一个人传染个人.10. 已知一个二次函数的图象开口向上,顶点坐标为(0,-1),则这个二次丽数的解析式可以为(写出一个即可).11. 抛物线y=-(x-h)2+k的部分图像如图所示,则此抛物线的顶点坐标是
 12. 若一元二次方程(x-3)2=1的两根为Rt△ABC的两直角边的长,则Rt△ABC的面积是13. 如图,抛物线y=ax2+bx+c与x轴相交于A,B(t+1,0)两点,与y轴相交于点C,点D在该抛物线上,且坐标为(t,c),则点A的横坐标是
12. 若一元二次方程(x-3)2=1的两根为Rt△ABC的两直角边的长,则Rt△ABC的面积是13. 如图,抛物线y=ax2+bx+c与x轴相交于A,B(t+1,0)两点,与y轴相交于点C,点D在该抛物线上,且坐标为(t,c),则点A的横坐标是 14. 已知函数y=ax2+2x+1的图像与坐标轴恰有两个公共点,则实数a的值是
14. 已知函数y=ax2+2x+1的图像与坐标轴恰有两个公共点,则实数a的值是三、解答题(每小题5分,共20分)
-
15. 解方程:16. 请利用公式法解方程:2x2+3x-1=0.17. 如图,已知在平面直角坐标系中,四边形OABC是边长为3的正方形,其中点A,C分别在x轴的正半轴和y轴的正半轴上,抛物线y=-x2+bx+c经过A,C两点求b,c的值.
 18. 为建设美丽城市,改造老旧小区,某市2020年投入资金1000万元,2022年投入资金1440万元.现假设每年投入资金的增长率相同,求该市投入资金的年平均增长率.
18. 为建设美丽城市,改造老旧小区,某市2020年投入资金1000万元,2022年投入资金1440万元.现假设每年投入资金的增长率相同,求该市投入资金的年平均增长率.四、解答题(每小题7分,共28分)
-
19. 将一条长为20cm的铁丝剪成两段,分别弯成两个正方形.(1)、若这两个正方形的面积之和为17cm2 , 分别求这两段铁丝的长.(2)、这两个正方形的面积之和能否为12cm2?若能,分别求这两段铁丝的长:若不能,请说明理由.20. 已知二次函数y=ax2+bx+c(a≠0).
 (1)、若a=-1,且函数图象经过(0,3),(2,-5)两点,求此二次函数的解析式.(2)、在图中画出(1)中函数的大致图像,并根据图像直接写出函数值y≥3时,自变量x的取值范围.21. 已知函数y=(1)、点P(2,2)在此函数的图象上.
(1)、若a=-1,且函数图象经过(0,3),(2,-5)两点,求此二次函数的解析式.(2)、在图中画出(1)中函数的大致图像,并根据图像直接写出函数值y≥3时,自变量x的取值范围.21. 已知函数y=(1)、点P(2,2)在此函数的图象上.①求n的值.
②求此函数的图象与y轴的交点,
(2)、当n=1时,此函数的最大值为22. 我国古代著作《四元玉鉴》记载“买椽多少"问题:“六贯二百一十钱,倩人去买几橼。每株脚钱三文足,无钱准与一株椽。”其大意为:现请人代买一批橡,这批椽的价钱为6210文。如果每株橡的运费是3文,那么少拿一株椽后,剩下的橡的运费恰好等于一株橡的价钱。求这批椽的数量。五、解答题(每小题8分,共16分)
-
23. 某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为15m),另外三面用栅栏围成,中间再用栅栏把它分成面积比为1:2的两个矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm(如图)。
 (1)、若矩形养殖场的总面积为36m2 , 求此时x的值。(2)、当x为多少时,矩形养殖场的总面积最大?最大值为多少?24. 设二次函数y1=2x2+bx+c(b,c是常数)的图像与x轴交于A,B两点。(1)、若A,B两点的坐标分别为(1,0),(2,0),则函数y1的解析式为 。(2)、若函数y1的解析式可以写成y1=2(x-h)2-2(h是常数)的形式,求b+c的最小值.(3)、设一次函数y2=x-n(n是常数)。若函数y1的解析式还可以写成y1=2(x-n)(x-n-2)的形式,当函数y=y1-y2的图像经过点(m,0)时,直接写出m-n的值。
(1)、若矩形养殖场的总面积为36m2 , 求此时x的值。(2)、当x为多少时,矩形养殖场的总面积最大?最大值为多少?24. 设二次函数y1=2x2+bx+c(b,c是常数)的图像与x轴交于A,B两点。(1)、若A,B两点的坐标分别为(1,0),(2,0),则函数y1的解析式为 。(2)、若函数y1的解析式可以写成y1=2(x-h)2-2(h是常数)的形式,求b+c的最小值.(3)、设一次函数y2=x-n(n是常数)。若函数y1的解析式还可以写成y1=2(x-n)(x-n-2)的形式,当函数y=y1-y2的图像经过点(m,0)时,直接写出m-n的值。六、解答题(每小题10分,共20分)
-
25. 如图①,在矩形ABCD中,AB=2cm,BC=4cm,动点P从点A出发,以1cm/s的速度沿边AD向终点D运动,同时动点Q从点A出发,以2cm/s的速度沿折线AB-BC-CD向终点D运动.设点P出发xs时,△APQ的面积为ycm2 . 已知y与x之间的函数关系如图②所示,其中MN为线段,曲线OM、NH为抛物线的一部分,请根据图中的信息,解答下列问题:
 (1)、m= , n= , k=(2)、分别求出曲线OM、线段MN所对应的函数解析式. (不要求写出自变量的取值范围)(3)、当x为何值时,△APQ的面积是2cm2?26. 如图,在平面直角坐标系中,抛物线y=-x2+b×+c(b,c是常数)经过点A(-1,0),点B(3,0),与y轴交于点C.
(1)、m= , n= , k=(2)、分别求出曲线OM、线段MN所对应的函数解析式. (不要求写出自变量的取值范围)(3)、当x为何值时,△APQ的面积是2cm2?26. 如图,在平面直角坐标系中,抛物线y=-x2+b×+c(b,c是常数)经过点A(-1,0),点B(3,0),与y轴交于点C. (1)、求此抛物线的解析式.(2)、若点P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P的坐标.(3)、在(2)的条件下,若点M为抛物线第一象限上的点,当S△BCM=S△BCP时,直接写出点M的横坐标.
(1)、求此抛物线的解析式.(2)、若点P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P的坐标.(3)、在(2)的条件下,若点M为抛物线第一象限上的点,当S△BCM=S△BCP时,直接写出点M的横坐标.