2022年秋季期浙教版九年级上册期中复习专题1 二次函数的图象与性质

试卷更新日期：2022-09-28 类型：复习试卷

进入出卷网下载

一、单选题

1. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列结论： $① 2 a + b = 0$ ；②若 $m$ 为任意实数，则 $a + b \geq a m^{2} + b m$ ； $③ a - b + c > 0$ ； $④ 3 a + c < 0$ ； $⑤$ 若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x_{2}$ ，且 $x_{1} \neq x_{2}$ ，则 $x_{1} + x_{2} = 2.$ 其中正确的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 将二次函数 $y = x^{2} + 4 x + 3$ 化成顶点式，变形正确的是（）

A、 $y = (x - 2)^{2} - 1$ B、 $y = (x + 1) (x + 3)$ C、 $y = (x - 2)^{2} + 1$ D、 $y = (x + 2)^{2} - 1$

查看试题解析
3. 如果二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，那么（）

A、 $a < 0$ ， $b > 0$ ， $c > 0$ B、 $a > 0$ ， $b < 0$ ， $c > 0$ C、 $a > 0$ ， $b < 0$ ， $c < 0$ D、 $a > 0$ ， $b > 0$ ， $c < 0$

查看试题解析
4. 二次函数 $y = a (x - 4)^{2} - 4 (a \neq 0)$ 的图象在 $2 < x < 3$ 这一段位于 $x$ 轴的下方，在 $6 < x < 7$ 这一段位于 $x$ 轴的上方，则 $a$ 的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
5. 抛物线 $y = x^{2} - 2 x + 1$ 的顶点坐标是（）

A、(1，0) B、(－1，0) C、(1，2) D、(－1，2)

查看试题解析
6. 如图是二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的一部分，对称轴为 $x = \frac{1}{2}$ 且经过点 $(2 ， 0) .$ 下列说法：
$① a b c < 0$ ； $② 4 a + 2 b + c < 0$ ； $③ - 2 b + c = 0$ ； $④$ 若 $(- \frac{5}{2} ， y_{1})$ ， $(\frac{5}{2} ， y_{2})$ 是抛物线上的两点，则 $y_{1} < y_{2}$ ； $⑤ \frac{1}{4} b > m (a m + b) ($ 其中 $m \neq \frac{1}{2}) .$ 其中说法正确的是（）

A、 $① ③ ④ ⑤$ B、 $① ② ④$ C、 $① ④ ⑤$ D、 $③ ④ ⑤$

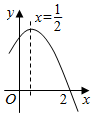查看试题解析
7. 在同一直角坐标系中，当 $a b > 0$ 时， $y = a x^{2}$ 与 $y = a x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 在平面直角坐标系中，不论m取何值时，抛物线 $y = x^{2} - 2 m x - 2 x + 2 m^{2} + 2 m + 2$ 的顶点一定在（）上.

A、 $y = x^{2}$ B、 $y = 2 x$ C、 $y = x^{2} + 1$ D、 $y = x^{2} - 2 x + 2$

查看试题解析
9. 点P（x₁ ， y₁），Q（x₂ ， y₂）在抛物线y＝ax²-4ax＋2（a＞0）上，若对于t＜x₁＜t＋1，t＋2＜x₂＜t＋3，都有y₁≠y₂ ，则t的取值范围是（）

A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-1

查看试题解析
10. 已知二次函数 $y = a x^{2} - 4 a x - 5 a + 1 (a > 0)$ 下列结论正确是（）
①已知点 $M (4 ， y_{1})$ ，点 $N (- 2 ， y_{2})$ 在二次函数的图象上，则 $y_{1} > y_{2}$ ；②该图象一定过定点 $(5 ， 1)$ 和 $(- 1 ， 1)$ ；③直线 $y = x - 1$ 与抛物线 $y = a x^{2} - 4 a x - 5 a + 1$ 一定存在两个交点；④当 $- 3 \leq x \leq 1$ 时， $y$ 的最小值是 $a$ ，则 $a = \frac{1}{10}$ ；

A、①④ B、②③ C、②④ D、①②③④

查看试题解析

二、填空题

11. 将二次函数 $y = 2 (x + 1)^{2}$ 的图象向右平移1个单位长度，再向下平移2个单位长度，所得新抛物线的解析式为．

查看试题解析
12. 抛物线 $y = - \frac{1}{2} {(x - 2)}^{2} + 5$ 的顶点坐标是.

查看试题解析
13. 已知二次函数y＝ax²＋bx＋c的图象的顶点坐标为（1，m），与y轴的交点为（0，m－2），则a的值为.

查看试题解析
14. 已知点P（x₀ ， m），Q（1，n）在二次函数y＝（x+a）（x﹣a﹣1）（a≠0）的图象上，且m＜n下列结论：①该二次函数与x轴交于点（﹣a，0）和（a+1，0）；②该二次函数的对称轴是x＝ $\frac{1}{2}$ ； ③该二次函数的最小值是（a+2）²； ④0＜x₀＜1．其中正确的是．（填写序号）

查看试题解析
15. 若直线y =ax+b（ab≠0）不经过第三象限，那么抛物线y=ax²+bx顶点在第象限.

查看试题解析
16. 如果将抛物线y＝x² $-$ 2x向上平移，使它经过点A（0，3），那么所得新抛物线的解析式是．

查看试题解析
17. 点P（m，n）在以y轴为对称轴的二次函数y=x²+ax+4的图象上，则m-n的最大值为.

查看试题解析
18. 已知抛物线y＝ax²﹣4ax+c（a≠0）与x轴交于A、B两点，若点A的坐标为（﹣2，0），则线段AB的长为．

查看试题解析

三、解答题

19. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 4 a x + 1$ .

(1)、若抛物线过点 $A (- 1, 6)$ ，求二次函数的表达式；

(2)、指出（1）中x为何值时y随x的增大而减小；

(3)、若直线 $y = m$ 与（1）中抛物线有两个公共点，求m的取值范围.

查看试题解析
20. 二次函数图象过A（﹣1，0），B（2，0），C（0，﹣2）三点，求此抛物线的解析式．

查看试题解析
21. 求抛物线y＝ $\frac{1}{2}$ x²﹣x＋1在﹣2≤x≤2的最大值与最小值．

查看试题解析
22. 如图，已知：关于y的二次函数 $y = x^{2} + b x + c$ 的图象与x轴交于点 $A (2 ， 0)$ 和点B，与y轴交于点 $C (0 ， 6)$ ，抛物线的对称轴与x轴交于点D.

(1)、求二次函数的表达式.

(2)、在y轴上是否存在一点P，使 $△ P B C$ 为直角三角形.若存在，请求出点P的坐标.

(3)、有一个点M从点A出发，以每秒1个单位的速度在 $A B$ 上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达B点时，点M、N同时停止运动，问点M、N运动到何处时， $△ M N B$ 面积最大，试求出面积.

查看试题解析
23. 某公司销售一种商品，成本为每件30元，经过市场调查发现，该商品的日销售量 $y$ （件）与销售单价 $x$ （元）是一次函数关系，其销售单价、日销售量的三组对应数值如下表：
销售单价 $x$ （元）
40
60
80
日销售量 $y$ （件）
80
60
40

(1)、求公司销售该商品获得的最大日利润；

(2)、销售一段时间以后，由于某种原因，该商品每件成本增加了10元，若物价部门规定该商品销售单价不能超过 $a$ 元，在日销售量 $y$ （件）与销售单价 $x$ （元）保持（1）中函数关系不变的情况下，该商品的日销售最大利润是1500元，求 $a$ 的值．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 与 $y$ 轴交于点 $C$ ，与 $x$ 轴交于 $A$ ， $B$ 两点 $($ 点 $A$ 在点 $B$ 的左侧 $)$ ，且 $A$ 点坐标为 $(- \sqrt{2} ， 0)$ ，直线 $B C$ 的解析式为 $y = - \frac{\sqrt{2}}{3} x + 2$ ．

(1)、求抛物线的解析式；

(2)、过点 $A$ 作 $A D / / B C$ ，交抛物线于点 $D$ ，点 $E$ 为直线 $B C$ 上方抛物线上一动点，连接 $C E$ ， $E B$ ， $B D$ ， $D C .$ 求四边形 $B E C D$ 面积的最大值及相应点 $E$ 的坐标；

(3)、将抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 向左平移 $\sqrt{2}$ 个单位，已知点 $M$ 为抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 的对称轴上一动点，点 $N$ 为平移后的抛物线上一动点．在（2）中，当四边形 $B E C D$ 的面积最大时，是否存在以 $A$ ， $E$ ， $M$ ， $N$ 为顶点的四边形为平行四边形？若存在，直接写出点 $N$ 的坐标；若不存在，请说明理由．

查看试题解析

销售单价 $x$ （元）	40	60	80
日销售量 $y$ （件）	80	60	40