人教版七上数学第二章2.2整式的加减课时易错题三刷（第三刷）

试卷更新日期：2022-09-27 类型：同步测试

进入出卷网下载

一、单选题

1. 若代数式 $a x^{2} + 4 x - y + 3 - (2 x^{2} - b x + 5 y - 1)$ 的值与x的取值无关，则 $a + b$ 的值为（）

A、6 B、－6 C、2 D、－2

查看试题解析
2. 如果a﹣4b＝0，那么多项式2（b﹣2a+10）+7（a﹣2b﹣3）的值是（）

A、﹣1 B、﹣2 C、1 D、2

查看试题解析

二、填空题

3. 已知A＝2x²+x+1，B＝mx+1，若关于x的多项式A+B不含一次项，则常数m＝．

查看试题解析
4. 已知有理数 $a$ ， $b$ ， $c$ 在数轴上对应的点的位置如图所示，化简 $| a + c | - | b - a | + | b - c | =$ .

查看试题解析
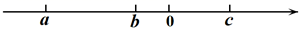5. 若单项式2x^my^m-n与单项式3x³y²ⁿ的和是5x^my²ⁿ ，则m-n的值是．

查看试题解析
6. 一个多项式与 $3 x^{2} - x - 1$ 的和是 $- x^{2} + x + 3$ ，则这个多项式是.

查看试题解析

三、计算题

7. 化简： $3 m^{2} - [2 m n^{2} - 3 (m n - \frac{2}{3} m n^{2}) + m^{2}] - 3 m n$ .

查看试题解析
8. 先化简下列各式，再求值：

(1)、（3x²y﹣4xy²）﹣（2x²y﹣3x²），其中x＝1，y＝﹣1；

(2)、3（x+y）²﹣5（x+y）+7（x+y）²+4（x+y），其中x+y＝﹣1．

查看试题解析

四、解答题

9. 已知：关于x、 $y$ 的多项式 $x^{2} + a x - y + b$ 与多项式 $b x^{2} - 3 x + 6 y - 3$ 的差的值与字母x的取值无关，求代数式 $3 (a^{2} - 2 a b - b^{2}) - (4 a^{2} + a b + b^{2})$ 的值.

查看试题解析
10. 已知关于x，y的式子 $(2 x^{2} + m x - y + 3) - (3 x - 2 y + 1 - n x^{2})$ 的值与字母x的取值无关，求式子 $(m + 2 n) - (2 m - n)$ 的值.

查看试题解析
11. 先化简，再求值： $2 (a^{2} - a b) - 3 (2 a^{2} - 3 a b) + 2 [a^{2} - (2 a^{2} - a b)] - 1$ ，其中a，b满足 $2 m^{3 a} n$ 和 $- 2 m^{6} n^{b + 2}$ 是同类项.

查看试题解析
12. 有理数a，b，c在数轴上的位置如图所示，且|a|＝|b|，化简|c－a|＋|c－b|＋|a＋b|.

查看试题解析

五、综合题

13. 已知： $A = 3 m x - x$ ， $B = - m x - 3 x + m$ .

(1)、化简： $3 A - 2 B$ ；

(2)、若 $3 A - 2 B$ 的值与字母m的取值无关，求x的值.

查看试题解析
14. 已知 $A = 2 a^{2} - 3 a + 1$ ， $B = a^{2} - 5 - 3 a$ .

(1)、当 $a = - 2$ 时，求代数式 $3 A - 2 (A - 2 B)$ 的值；

(2)、试判断 $A$ 、 $B$ 的大小关系，并说明理由.

查看试题解析
15. 亮亮在计算多项式A减多项式 $2 b^{2} - 3 b - 5$ 时，因一时疏忽忘了将两个多项式用括号括起来，计算成了 $A - 2 b^{2} - 3 b - 5$ ，得到的结果是 $b^{2} + 3 b - 1$ .

(1)、求这个多项式A；

(2)、求这两个多项式相减的正确结果，并求 $b = - 1$ 时正确结果的值.

查看试题解析
16. 小亮做一道数学题“两个多项式A和B，B为 $4 x^{2} - 5 x - 7$ ，试求 $A + 2 B$ 的值”.小亮误将 $A + 2 B$ 看成 $A - 2 B$ ，结果答案（计算正确）为 $- 2 x^{2} + 10 x + 14$ .

(1)、试求 $A + 2 B$ 的正确结果；

(2)、求出当 $x = - 1$ 时， $A + 2 B$ 的值.

查看试题解析
17. 有理数a、b、c在数轴上的位置如图：

(1)、用“＞”或“＜”填空：a 0，b 0，c -a 0.

(2)、化简： $| a | + | b - c | - | c - a |$ .

查看试题解析
18. “整体思想”是中学数学学习中的一种重要思想，它在多项式的化简与求值中应用极为广泛，例如把 $(a + b)$ 看成一个整体： $4 (a + b) + 3 (a + b) = (4 + 3) (a + b) = 7 (a + b)$ ，请应用整体思想解答下列问题：

(1)、化简： $5 {(m + n)}^{2} - 7 {(m + n)}^{2} + 3 {(m + n)}^{2}$ ；

(2)、已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值.

查看试题解析

人教版七上数学第二章2.2整式的加减 课时易错题三刷（第三刷）

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

人教版七上数学第二章2.2整式的加减课时易错题三刷（第三刷）