山东省淄博市淄川区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. “小明同学期中考试得满分”这是一个（）

A、必然事件 B、不可能事件 C、随机事件 D、确定事件

查看试题解析
2. 对于等式3x﹣2y=5，用含x的代数式来表示y，下列式子正确的是（　　）

A、 $y = \frac{5 - 3 x}{2}$ B、 $x = \frac{2 y - 5}{2}$ C、 $x = \frac{5 - 2 y}{2}$ D、 $y = \frac{3 x - 5}{2}$

查看试题解析
3. 如图， $a // b$ ，若∠1＝2∠2，则∠2的度数为（）

A、50° B、60° C、70° D、80°

查看试题解析
4. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形，任意转动这4个转盘各1次．转盘停止转动时，指针落在阴影区域的可能性最大的转盘是（　　）

A、 B、 C、 D、

查看试题解析
5. 若单项式2x²y^a+b与- $\frac{1}{3}$ x^a-by⁴是同类项，则a，b的值分别为（）

A、a＝3，b＝1 B、a＝-3，b＝1 C、a＝3，b＝-1 D、a＝-3，b＝-1

查看试题解析
6. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - y = 4 ， \\ k x + y = 2 \end{array}$ ，的解为 ${\begin{array}{l} x = 2 ， \\ y = ♥ \end{array}$ ，其中“♥”是不小心被墨水涂的，则k的值为（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
7. 一个零件的形状如图所示， $A B / / D E ， A D / / B C ， ∠ C B D = 60^{°} ， ∠ B D E = 40^{°}$ ，则 $∠ A$ 的度数是（）

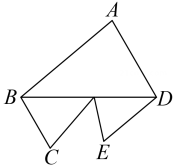A、70° B、80° C、90° D、100°

查看试题解析
8. 甲、乙、丙3个学生分别在A、B、C三所大学学习数学、物理，化学中的一个专业，且满足：①甲不在A校学习；②乙不在B校学习；③在B校学习的学数学；④在A校学习的不学化学；⑤乙不学物理.则（）

A、甲在C校学习，丙在B校学习 B、甲在B校学习，丙在C校学习 C、甲在B校学习，丙在A校学习 D、甲在C校学习，丙在A校学习

查看试题解析
9. 如图，将一副三角板如图所示摆放，其中点F在 $A C$ 上， $∠ E F D = 90 °$ ， $∠ D E F = 45 °$ ， $A B ∥ D E$ ，则 $∠ A F D$ 等于（）

A、15° B、30° C、12° D、35°

查看试题解析
10. 现有两种礼包，甲种礼包里面含有 $4$ 个毛绒玩具和 $1$ 套文具.乙种礼包里面含有 $3$ 个毛绒玩具和 $2$ 套文具.现在需要 $37$ 个毛绒玩具， $18$ 套文具，则需要采购甲种礼包的数量为（）

A、 $2$ 件 B、 $3$ 件 C、 $4$ 件 D、 $5$ 件

查看试题解析
11. 如图，在边长为1的3×3的正方形网格中，网格线的交点称为格点．已知A，B是格点，在格点上任意放置点C，恰好能使 $△ A B C$ 的面积为1的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{5}{12}$ D、 $\frac{1}{2}$

查看试题解析
12. A，B两地相距100 km，甲、乙两人骑车同时分别从A，B两地相向而行．假设他们都保持匀速行驶，则他们各自到A地的距离 $s (k m)$ 都是骑车时间 $t (h)$ 的一次函数，其图像如图所示．已知1 h后乙距离A地80 km，2 h后甲距离A地30 km，则经过多长时间两人将相遇？（）

A、3 h B、 $\frac{20}{7} h$ C、 $\frac{7}{2} h$ D、4 h

查看试题解析

二、填空题

13. 命题“同旁内角互补，两直线平行”的条件是．

查看试题解析
14. 如图，请你添加一个条件，可以得到 $D E ∥ A C$ ．

查看试题解析
15. 语言是思维的工具，要学好几何证明，必须学会语言的表达和运用．几何语言可分为文字语言、符号语言与图形语言．例知：“直线a与b互相平行”是文字语言，“ $a ∥ b$ ”是符号语言，那么“直线a与b互相平行”的图形语言是．

查看试题解析
16. 请写出一个二元一次方程组，使该方程组无解．你写的方程组是．

查看试题解析
17. 为了解某地区七年级男生的身高情况，随机抽取了该地区100名七年级男生，他们的身高 $x c m$ 统计如下：
组别
小于160
大于160（含160）而小于170
大于170（含170）而小于180
大于180（含180）
人数
15
38
42
5
根据以上结果，抽查该地区一名七年级男生，估计他的身高不低于180 cm的概率是．

查看试题解析
18. 若实数a，b既满足 $a + 2 b = 2$ ，又满足 $3 a + 4 b = 26$ ，则 $a + b =$ ．

查看试题解析
19. 一个不透明的袋子中装有红、黄、白三种颜色的球共100个，它们除颜色外其余都相同，其中黄球个数是白球个数的2倍少5个，已知从袋中摸出一个球是红球的概率是 $\frac{3}{10}$ ，则从袋中摸出一个球是黄球的概率是．

查看试题解析
20. 在代数式 $a x^{2} + b x$ 中，当 $x = - 1$ ， 2时，代数式的值依次是0， $- 6$ ，则当 $x = 1$ 时，这个代数式的值是．

查看试题解析

三、解答题

21.

(1)、将下列命题写成“如果……那么……”的形式，并指出它们是真命题还是假命题．
①在同一平面内，垂直于同一直线的两条直线平行；
②两个锐角的和是钝角；
③内错角相等，两直线平行；
④负数小于0．

(2)、已知：如图，在 $△ A B C$ 中， $∠ B = ∠ C$ ， $A D$ 平分外角 $∠ E A C$ ．
求证： $A D ∥ B C$ ．

(3)、用10个除颜色外完全相同的球设计摸球游戏．你是怎么设计的？
①使得摸到红球的概率是 $\frac{1}{2}$ ，摸到白球的概率也是 $\frac{1}{2}$ ：
②使得摸到红球的概率是 $\frac{1}{5}$ ，摸到白球和黄球的概率都是 $\frac{2}{5}$ ．

查看试题解析
22.

(1)、解方程组：
① ${\begin{array}{l} 3 a + b = 3 ， \\ 8 a - 4 b = 28 . \end{array}$

② ${\begin{array}{l} 2 x - 3 y - 2 = 0 ， \\ \frac{2 x - 3 y + 5}{7} + 2 y = 9 . \end{array}$

(2)、①如图，已知 $A B = A_{1} B$ ， $A_{1} C = A_{1} A_{2}$ ， $A_{2} D = A_{2} A_{3}$ ， $A_{3} E = A_{3} A_{4}$ ， $∠ B = 20 °$ ，求 $∠ A_{4}$ 的度数．

②在①的条件下，根据你获得的计算经验，以此类推…，若 $∠ B = α$ ，请直接写出用含 $α$ 的代数式表示 $∠ A_{n}$ 的度数．

查看试题解析
23. 某工厂去年的利润（总产值－总支出）为200万元，今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润比去年的利润增加了580万元．问今年的总产值、总支出各是多少万元？

查看试题解析
24. 已知：如图，BP交CD于点P，∠ABP+∠BPC=180°，EB $∥$ PF．
求证：∠1=∠2．

查看试题解析
25. 暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下.
方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；

方案二：不购买学生暑期专享卡，每次健身费用按八折优惠；

设某学生暑期健身x(次)，按照方案一所需费用为 $y_{1}$ ，(元)，且 $y_{1} = k_{1} x + b$ ；按照方案二所需费用为 $y_{2}$ (元) ，且 $y_{2} = k_{2} x .$ 其函数图象如图所示.

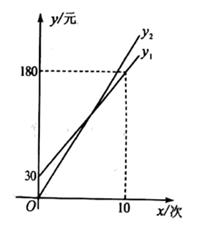(1)、求 $k_{1}$ 和b的值，并说明它们的实际意义；

(2)、求打折前的每次健身费用和 $k_{2}$ 的值；

(3)、八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少?说明理由.

查看试题解析

组别	小于160	大于160（含160）而小于170	大于170（含170）而小于180	大于180（含180）
人数	15	38	42	5