山东省淄博市张店区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 在代数式 $\frac{m - n}{4}$ ， $\frac{x^{2}}{x}$ ， ﹣3x， $\frac{3 x}{π}$ ， $\frac{2}{a + b}$ 中，其中是分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 式子 $\frac{1}{x - 2}$ 有意义，则x满足的条件是（）

A、x≠0 B、x＞0 C、x＞2 D、x≠2

查看试题解析
3. 下列各式分解因式结果是(a−2)(b+3)的是（）

A、−6+2b−3a+ab B、−6−2b+3a+ab C、ab−3b+2a−6 D、ab−2a+3b−6

查看试题解析
4. 如果二次三项式 $x^{2} + a x + 2$ 可分解为 $(x - 1) (x + b)$ ，则 $a + b$ 的值为（）

A、 $- 2$ B、 $- 5$ C、3 D、5

查看试题解析
5. 小东是一位密码爱好者，在他的密码手册中有这样一条信息： $a - b$ 、 $a + b$ 、 $a^{2} - b^{2}$ 、 $c - d$ 、 $c + d$ 、 $c^{2} - d^{2}$ 依次对应下列六个字：科、爱、勤、我、理、学，现将 $(a^{2} - b^{2}) c^{2} - (a^{2} - b^{2}) d^{2}$ 因式分解，其结果呈现的密码信息可能是（）．

A、勤学 B、爱科学 C、我爱理科 D、我爱科学

查看试题解析
6. 若分式 $\frac{x^{2} - 9}{x^{2} - 4 x + 3}$ 的值为零，那么（）

A、 $x = 3$ 或 $x = - 3$ B、 $x = 3$ 且 $x = - 3$ C、 $x = 3$ D、 $x = - 3$

查看试题解析
7. “新冠病毒”的英语“Novelcoronavirus”中，字母“n”出现的频率是（　　）

A、 $\frac{1}{16}$ B、 $\frac{1}{8}$ C、2 D、1

查看试题解析
8.
下图是甲、乙两户居民家庭全年支出费用的扇形统计图．

根据统计图，下面对全年食品支出费用判断正确的是（）

A、甲户比乙户多 B、乙户比甲户多 C、甲、乙两户一样多 D、无法确定哪一户多

查看试题解析
9. 已知关于x的分式方程 $\frac{m}{x - 1}$ + $\frac{3}{1 - x}$ =1的解是非负数，则m的取值范围是（）

A、m＞2 B、m≥2 C、m≥2且m≠3 D、m＞2且m≠3

查看试题解析
10. 现有一列数： $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， …， $a_{n - 1}$ ， $a_{n}$ （ $n$ 为正整数），规定 $a_{1} = 2$ ， $a_{2} - a_{1} = 4$ ， $a_{3} - a_{2} = 6$ ， …， $a_{n} - a_{n - 1} = 2 n (n \geq 2)$ ，若 $\frac{1}{a_{2}} + \frac{1}{a_{3}} + \frac{1}{a_{4}} \cdot \cdot \cdot \frac{1}{a_{n}} = \frac{97}{198}$ ，则n的值为（）

A、97 B、98 C、99 D、100

查看试题解析
11. “五•一”江北水城文化旅游节期间，几名同学包租一辆面包车前去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，设原来参加游览的同学共x人，则所列方程为（）

A、 $\frac{180}{x - 2}$ ﹣ $\frac{180}{x}$ ＝3 B、 $\frac{180}{x + 2}$ ﹣ $\frac{180}{x}$ ＝3 C、 $\frac{180}{x}$ ﹣ $\frac{180}{x - 2}$ ＝3 D、 $\frac{180}{x} - \frac{180}{x + 2} = 3$

查看试题解析
12. 任何一个正整数n都可以进行这样的分解： $n = s \times t$ （s，t是正整数，且 $s \leq t$ ）如果 $p \times q$ 在n的所有这种分解中两因数之差的绝对值最小，我们就称 $p \times q$ 是n的最佳分解，并规定： $F (n) = \frac{p}{q}$ ．例如18可以分解成 $1 \times 18$ ， $2 \times 9$ ， $3 \times 6$ 这三种，这时就有 $F (18) = \frac{3}{6} = \frac{1}{2}$ ，给出下列关于 $F (n)$ 的说法：① $F (2) = \frac{1}{2}$ ；② $F (24) = \frac{3}{8}$ ；③ $F (27) = 3$ ；④若n是一个整数的平方，则 $F (n) = 1$ ，其中正确说法的有（）

A、①② B、①③ C、①④ D、②④

查看试题解析

二、填空题

13. 若代数式 $\frac{2}{a - 2}$ 有意义，则实数a的取值范围是．

查看试题解析
14. 已知x²﹣x-1=0，那么代数式x³﹣2x+1的值是．

查看试题解析
15. 关于x的分式方程 $\frac{2}{x - 1} + \frac{kx}{x^{2} - 1} = \frac{3}{x + 1}$ 会产生增根，则k＝.

查看试题解析
16. 开学前，根据学校防疫要求，小明同学连续14天进行了体温测量，结果统计如下表：

体温（℃）

36.3

36.4

36.5

36.6

36.7

36.8

天数（天）

2

3

3

4

1

1

这组体温数据的中位数是℃.

查看试题解析
17. 若n为正整数，观察下列各式：
① $\frac{1}{1 \times 3} = \frac{1}{2} (1 - \frac{1}{3})$ ；
② $\frac{1}{3 \times 5} = \frac{1}{2} (\frac{1}{3} - \frac{1}{5})$ ；
③ $\frac{1}{5 \times 7} = \frac{1}{2} (\frac{1}{5} - \frac{1}{7})$ …根据观察计算并填空：

(1)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} =$ ．

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + ⋯ \frac{1}{(2 n - 1) (2 n + 1)} =$ ．

查看试题解析

三、解答题

18. 将下列多项式进行因式分解：

(1)、 $4 x^{3} - 24 x^{2} y + 36 x y^{2}$ ；

(2)、 $x^{2} (y - 4) + 9 (4 - y)$ ．

查看试题解析
19. 化简求值： $(2 + \frac{1}{a - 1} - \frac{1}{a + 1}) \div (a - \frac{a}{1 - a^{2}})$ ，其中 $a = 2$ ．

查看试题解析
20. 解方程：

(1)、 $\frac{4}{x^{2} - 4} = \frac{1}{x - 2} - 1$

(2)、 $\frac{1}{x - 2} + 2 = \frac{1 - x}{2 - x}$

查看试题解析
21. 为加强安全教育，某校开展了“预防水，珍爱生命”安全知识竞赛，现从七，八，九年级学生中随机抽取了50名学生进行竞赛，并将他们的竞赛成绩（百分制）进行了整理和分析，部分信息如下：
a．参赛学生成绩频数分布直方图（数据分成五组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）如图所示；
b．参赛学生成绩在 $70 < x < 80$ 这一组的具体得分是：70，71，73，75，76，76，76，77，77，78，79．
c．参赛学生成绩的平均数、中位数、众数如下：
平均数
中位数
众数
76.9
m
80
d．参赛学生甲的竞赛成绩得分为79分．
根据以上信息，回答下列问题：

(1)、在这次竞赛中，成绩在75分以上的有人；

(2)、表中m的值为．

(3)、该校学生共有1500人，假设全部参加此次竞赛，请估计成绩超过平均数76.9分的人数．

查看试题解析
22. 如图1，在一个边长为 $a$ 的正方形中，剪去一个边长为 $b$ 的小正方形，再将余下的部分拼成如图2所示的长方形．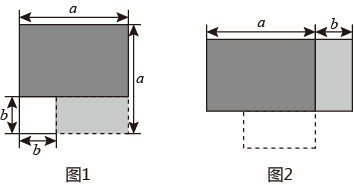

(1)、（观察）
比较两图中阴影部分的面积，可以得到等式：（用字母 $a$ ， $b$ 表示）；

(2)、（应用）
计算： $(x - 3) (x + 3) (x^{2} + 9)$ ；

(3)、（拓展）
已知 $2 m - n = 3$ ， $2 m + n = 4$ ，求 $8 m^{2} - 2 n^{2}$ 的值．

查看试题解析
23. 倡导健康生活推进全民健身，德州某社区去年购进A，B两种健身器材若干件，经了解，B种健身器材的单价是A种健身器材的1.5倍，用6000元购买A种健身器材比用3600元购买B种健身器材多15件．

(1)、A，B两种健身器材的单价分别是多少元？

(2)、若今年两种健身器材的单价和去年保持不变，该社区计划再购进A，B两种健身器材共60件，且费用不超过17600元，请问：A种健身器材至少要购买多少件？

查看试题解析
24. 给出如下规定：若实数 $a$ 与 $b$ 的差等于这两个数的积，则称实数对 $(a ， b)$ 为“关联数”.如实数对 $(- 2 ， 2)$ ，因为 $- 2 - 2 = - 4$ ， $(- 2) \times 2 = - 4$ ，所以实数对 $(- 2 ， 2)$ 是关联数；又如实数对 $(0 ， 0)$ 是关联数.

(1)、若实数对 $(a ， b)$ 为“关联数”，则 $a$ ， $b$ 应满足的条件用含 $a$ ， $b$ 的等式表示为.

(2)、判断下列实数对是否是关联数？
① $(1 ， - \frac{1}{2})$ ；

② $(- \frac{3}{4} ， - 3)$ .

(3)、若实数对 $(\frac{2 x - 1}{2} ， - 5)$ 是关联数，求 $x$ 的值.

(4)、是否存在非零实数 $m$ ， $n$ ，使实数对 $(2 m ， 3 n)$ 与 $(3 m ， 2 n)$ 都是关联数？若存在，求出 $m$ ， $n$ 的值；若不存在，请说明理由.

查看试题解析

体温（℃）	36.3	36.4	36.5	36.6	36.7	36.8
天数（天）	2	3	3	4	1	1

平均数	中位数	众数
76.9	m	80