山东省淄博市桓台县2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式① $x^{2} - 16 = (x + 4) (x - 4)$ ；② ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ； ③ $a^{2} b - a b^{2} = a b (a - b)$ ．从左边到右边的变形中，是因式分解的为（）

A、①③ B、①② C、② D、②③

查看试题解析
2. 若分式 $\frac{x - 2}{x + 3}$ 的值为零，则x为（）

A、 $x = 2$ B、 $x = - 3$ C、 $x = - 2$ D、 $x = 2$ 或 $x = - 3$

查看试题解析
3. 下列分式是最简分式的是（）

A、 $\frac{2 a}{3 a^{2} b}$ B、 $\frac{2 a}{4 b}$ C、 $\frac{a + b}{a^{2} + b^{2}}$ D、 $\frac{a^{2} - a b}{a^{2} - b^{2}}$

查看试题解析
4. 若 $\frac{a}{b} = M (a \neq b)$ ，则M可以是（　　）

A、 $\frac{a - 2}{b - 2}$ B、 $\frac{a + 2}{b + 2}$ C、 $\frac{- a}{- b}$ D、 $\frac{a^{2}}{b^{2}}$

查看试题解析
5. 若 $3 b = 2 a + 3$ ，则代数式 $4 a^{2} - 12 a b + 9 b^{2}$ 的值为（）

A、 $- 1$ B、9 C、7 D、5

查看试题解析
6. 若 $\frac{(1 0^{2} - 1) (1 2^{2} - 1)}{k} = 9 \times 11 \times 13$ ，则 $k =$ （）

A、12 B、11 C、10 D、9

查看试题解析
7. 已知样本 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …， $x_{n}$ 的方差是1，则样本 $2 x_{1} + 3$ ， $2 x_{2} + 3$ ， $2 x_{3} + 3$ ， …， $2 x_{n} + 3$ 的方差是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 小明的数学平时成绩为94分，期中成绩为92分，期末成绩为96分，若按3：3：4的比例计算总评成绩，则小明的数学总评成绩为（）

A、93 B、94 C、94.2 D、95

查看试题解析
9. 计算 ${(- 2)}^{2021} + {(- 2)}^{2022}$ ，所得结果是（）

A、 $2^{2021}$ B、 $- 2$ C、 $- 2^{2021}$ D、 $- 1$

查看试题解析
10. 若2x﹣5是多项式4x²+mx﹣5（m为系数）的一个因式，则m的值是（）

A、8 B、﹣6 C、﹣8 D、﹣10

查看试题解析
11. 如图所示，大长方形中放入5张长为 $x$ ，宽为 $y$ 的相同的小长方形，其中 $A$ ， $B$ ， $C$ 三点在同一条直线上.若阴影部分的面积为52，大长方形的周长为36，则一张小长方形的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
12. 某校“英语课本剧”表演比赛中，九年级的10名学生参赛成绩统计如图所示，对于这10名学生的参赛成绩，下列说法中正确的是（）

A、平均数是88 B、众数是85 C、中位数是90 D、方差是6

查看试题解析

二、填空题

13. 如果分式 $\frac{x + 1}{| x | - 1}$ 有意义，则x的取值范围是．

查看试题解析
14. 当 $a = 2 - b$ 时，计算 $(a - \frac{b^{2}}{a}) \div \frac{a - b}{a}$ 的值为．

查看试题解析
15. 一个矩形的两边长分别为a，b，其周长为14，面积是12，则ab²+a²b的值为．

查看试题解析
16. 如图，点A，B在数轴上，它们对应的数分别为-2， $\frac{x}{x + 1}$ ，且点A，B关于原点对称，则x的值是．

查看试题解析
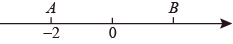17. 已知一组数据5，2，x，6，4，它们的平均数是4，则这组数据的标准差为．

查看试题解析

三、解答题

18. 因式分解

(1)、 $y (y + 4) - 4 (y + 1)$

(2)、 ${(a^{2} + b^{2})}^{2} - 4 a^{2} b^{2}$

查看试题解析
19. 计算

(1)、 $\frac{x^{2}}{x + 1} - x + 1$

(2)、 $\frac{3 - x}{x - 2} \div (x - 2 - \frac{3}{x - 2})$

查看试题解析
20. 已知，整式 $A = x (x + 3) + 5$ ，整式 $B = a x - 1$ ．

(1)、若 $A + B = {(x + 2)}^{2}$ ，求a的值；

(2)、若 $A - B$ 可以分解为 $(x - 2) (x - 3)$ ，请将 $A + B - 16$ 进行因式分解．

查看试题解析
21. 解分式方程

(1)、 $\frac{2 - x}{x - 3} = \frac{1}{3 - x} - 2$

(2)、 $\frac{x}{x - 2} - 1 = \frac{6}{x^{2} - 4}$

查看试题解析
22. 先化简，再求值： $(\frac{x - 1}{x^{2} - 4 x + 4} - \frac{x + 2}{x^{2} - 2 x}) \div (\frac{4}{x} - 1)$ ，其中x是不等式 $\frac{2 x - 5}{3}$ ≤x﹣3的最小整数解．

查看试题解析
23. 某文具店王老板用240元购进一批笔记本，很快售完；王老板又用600元购进第二批笔记本，所购本数是第一批的2倍，但进价比第一批每本多了2元．

(1)、第一批笔记本每本进价多少元？

(2)、王老板以每本12元的价格销售第二批笔记本，售出60%后，为了尽快售完，决定打折促销，要使第二批笔记本的销售总利润不少于48元，剩余的笔记本每本售价最低打几折？

查看试题解析

24. 为选派一名学生参加全市实践活动技能竞赛，A，B两位同学在校实习基地现场进行加工直径为20mm的零件的测试，他俩加工的10个零件的相关数据依次如下图表所示（单位：mm）．

根据测试得到的有关数据，试解答下列问题：

	平均数	方差	完全符合要求的个数
A	20	0.026	2
B	20	S²B	5

(1)、考虑平均数与完全符合要求的个数，你认为的成绩好些．

(2)、计算出SB²的大小，考虑平均数与方差，说明谁的成绩好些．

(3)、考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．

查看试题解析