山东省枣庄市台儿庄区2021-2022学年八年级上学期期中考试数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法错误的是（）

A、1的平方根是 $± 1$ B、 $- 1$ 的立方根是 $- 1$ C、 $\pm \sqrt{2}$ 是2的平方根 D、 $- 3$ 是 $\sqrt{(- 3)^{2}}$ 的平方根

查看试题解析
2. 下列计算中，正确的是（）

A、 $\sqrt{3} + \sqrt{4} = \sqrt{7}$ B、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ C、 $\sqrt{(- 2)^{2}} = - 2$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
3. 满足下列条件时，△ABC不是直角三角形的为（　　）

A、AB＝ $\sqrt{41}$ ， BC＝4，AC＝5 B、AB：BC：AC＝3：4：5 C、∠A：∠B：∠C＝3：4：5 D、∠A =15°，∠B =75°

查看试题解析
4. 若 $a = \sqrt[3]{7}$ ， $b = \sqrt{5}$ ， $c = 2$ ，则a ， b ， c的大小关系为（）

A、 $b < c < a$ B、 $b < a < c$ C、 $a < c < b$ D、 $a < b < c$

查看试题解析
5. 计算： $(\frac{\sqrt{5} + 1}{2} - 1) \cdot \frac{\sqrt{5} + 1}{2} =$ （）

A、0 B、1 C、2 D、 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
6. 如图，已知校门的坐标是 $(1 ， 1)$ ，那么下列对于实验楼位置的叙述：①实验楼的坐标是3；②实验楼的坐标是 $(3 ， 3)$ ；③实验楼的坐标为 $(4 ， 4)$ ④实验楼在校门的东北方向上，距校门200米．其中正确的有（）
比例尺：1：10000（单位：厘米）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在矩形ABCD中，AB＝5，AD＝3，点E为BC上一点，把△CDE沿DE翻折，点C 恰好落在AB边上的F处，则CE的长是（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

查看试题解析
8. 若直线 $y = - 7 x + 3$ 与直线 $y = 2 x + b$ 都经过y轴同一点，则b的值为（）

A、7 B、-7 C、3 D、-3

查看试题解析
9. 如图，从一个大正方形中截去面积为 $3 {cm}^{2}$ 和 $12 {cm}^{2}$ 的两个小正方形，若随机向大正方形内投一粒米，则米粒落在图中阴影部分的概率为（）

A、 $\frac{4}{9}$ B、 $\frac{5}{9}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
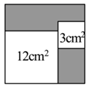10. 甲乙两车从A城出发前往B城，在整个行程中，汽车离开A城的距离y与时刻t的对应关系如图所示，则下列结论错误的是（）.

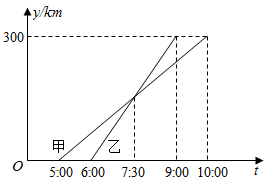A、甲车的平均速度为 $60 k m / h$ B、乙车的平均速度为 $100 k m / h$ C、乙车比甲车先到 $B$ 城 D、乙车比甲车先出发 $1 h$

查看试题解析
11. 如图，在平面直角坐标系中，点 $A (2 ， m)$ 在第一象限，若点A关于x轴的对称点B在直线y=-x+1上，则m的值为（）

A、-1 B、1 C、2 D、3

查看试题解析
12. 如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG＝3，CG＝2，则CE的长为（　　）

A、 $\frac{5}{4}$ B、 $\frac{15}{4}$ C、4 D、 $\frac{9}{2}$

查看试题解析

二、填空题

13. 一个正数a的两个平方根是 $2 b - 1$ 和 $b + 4$ ，则 $a + b$ 的立方根为．

查看试题解析
14. 如图所示，正方形ABCD的边长为4，点A的坐标为(-1，1)，AB平行于x轴，则点C的坐标为．

查看试题解析
15. 已知 $a = \sqrt{3} - \sqrt{2}$ ， $b = \sqrt{3} + \sqrt{2}$ ，则 $a^{2021} \cdot b^{2022} =$ ．

查看试题解析
16. 已知直线l与直线 $y = - 2 x$ 平行，且与y轴交于点（0，2），直线l的表达式为．

查看试题解析
17. 比较大小： $\frac{\sqrt{5} - 1}{2}$ $\frac{5}{8}$ （填“＞”、“＜”或“＝”）．

查看试题解析
18. 如图所示，将边长为2的等边三角形沿 $x$ 轴正方向连续翻折2021次，依次得到P₁ ， P₂ ， P₃ ， $\dots$ P₂₀₂₁ ，则点P₂₀₂₁的坐标是．

查看试题解析

三、解答题

19.

(1)、 $\sqrt{(- 2)^{2}} - \sqrt{2 \frac{1}{4}} + \sqrt[3]{\frac{7}{8} - 1} - \sqrt[3]{- 1}$

(2)、 $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}} + | 2 - \sqrt{5} |$

(3)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

(4)、 $\frac{\sqrt{20} + \sqrt{5}}{\sqrt{5}} - \sqrt{\frac{1}{3}} \times \sqrt{12} + (\sqrt{3} + 1) (\sqrt{3} - 1)$

查看试题解析
20. 在平面直角坐标系中，已知点A（﹣3，2），B（﹣1，0），C（﹣2，﹣1）．

(1)、请在图中画出△ABC，并画出与△ABC关于y轴对称的图形．

(2)、试判定△ABC的形状，并说明理由．

查看试题解析
21. 如图，在四边形ABCD中，AB=13，BC=5，CD=15，AD=9，对角线AC⊥BC．

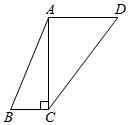(1)、求AC的长；

(2)、求四边形ABCD的面积．

查看试题解析
22. 阅读例题，然后回答问题：
例题：设a，b为有理数，且满足 $a + \sqrt{2} b = 3 - 2 \sqrt{2}$ ，求 $a + b$ 的值．
解：由题意得： $a - 3 + (b + 2) \sqrt{2} = 0$ ，因为a，b为有理数，所以 $a - 3$ ， $b + 2$ 也是有理数，所以 $a = 3$ ， $b = - 2$ ，所以 $a + b = 3 + (- 2) = 1$ ．
问题：设x，y为有理数，且满足 $x^{2} - 2 y + \sqrt{5} y = 10 + 3 \sqrt{5}$ ，求 $x^{y}$ 的值．

查看试题解析
23. 如图，一次函数y=-x+m的图象和y轴交于点B，与正比例函数y=x图象交于点P （2，n）．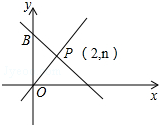

(1)、求m和n的值；

(2)、求△POB的面积．

查看试题解析
24. 图1，小刚家，学校、图书馆在同一条直线上，小刚骑自行车匀速从学校到图书馆，到达图书馆还完书后，再以相同的速度原路返回家中（上、下车时间忽略不计）．小刚离家的距离 $y (m)$ 与他所用的时间 $x (m i n)$ 的函数关系如图2所示．

(1)、小刚家与学校的距离为m，小刚骑自行车的速度为 $m / m i n$ ；

(2)、求小刚从图书馆返回家的过程中，y与x的函数表达式；

(3)、小刚出发35分钟时，他离家有多远?

查看试题解析
25. 如图，E、F是等腰Rt△ABC的斜边BC上的两动点，∠EAF=45°，CD⊥BC且CD=BE ．

(1)、求证：△ABE≌△ACD；

(2)、求证：EF²=BE²+CF² ．

查看试题解析