山东省枣庄市市中区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 木工师傅想利用木条制作一个直角三角形的工具，那么下列各组数据不符合直角三角形的三边长的是（　　）.

A、3，4，5 B、6，8，10 C、5，12，13 D、13，16，18

查看试题解析
2. 在实数0.3，0， $\sqrt{7}$ ， $\frac{π}{2}$ ， $\frac{\sqrt{10}}{2}$ ， 123454545…中，无理数有（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 如果点 $A (m ， 2)$ 和点 $B (3 ， n)$ 关于 $y$ 轴对称，则 $m$ 、 $n$ 的值为（）

A、 $m = - 3$ ， $n = - 2$ B、 $m = - 3$ ， $n = 2$ C、 $m = 3$ ， $n = 2$ D、 $m = 3$ ， $n = - 2$

查看试题解析
4. 下列各式① $y = - 8 x$ ；② $y = - \frac{3}{x}$ ；③ $y = \sqrt{x} + 1$ ；④ $y = - 8 x^{2} + 2$ ；⑤ $y = 0.5 x - 3$ ．是一次函数的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 小风在1000米中长跑训练时，已跑路程x（米）与所用时间t（秒）之间的函数图象如图所示，下列说法错误的是（）

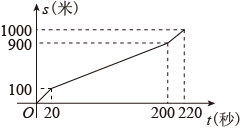A、小风的成绩是220秒 B、小风最后冲刺阶段的速度是5米/秒 C、小风第一阶段与最后冲刺阶段速度相等 D、小风的平均速度是4米/秒

查看试题解析
6. 下列运算中错误的有是（　　）

A、 $\sqrt{16} = 4$ B、 $\sqrt[3]{- 3^{2}} = 3$ C、 $\sqrt{{(- 3)}^{2}} = 3$ D、 $\sqrt[3]{(- 8)^{2}} = 4$

查看试题解析
7. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是2，3，4，5，6，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（　　）

A、2，4，6 B、2，3，5 C、3，3，6 D、2，2，4

查看试题解析
8. 实数 $a 、 b$ 在数轴上对应点的位置如图所示，化简 $| a | - \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、 $- 2 a + b$ B、 $2 a - b$ C、 $- b$ D、 $b$

查看试题解析
9. 已知 $y = \sqrt{2 x - 5} + \sqrt{5 - 2 x} - 3$ ，则 $2 x y$ 的值为（）

A、 $- 15$ B、 $15$ C、 $- \frac{15}{2}$ D、 $\frac{15}{2}$

查看试题解析
10. 如图，在△ABC中，AB=AC=13，BC=10，点D为BC的中点，DE⊥AB，垂足为点E，则DE等于（）

A、 $\frac{10}{13}$ B、 $\frac{15}{13}$ C、 $\frac{45}{13}$ D、 $\frac{60}{13}$

查看试题解析
11. 在如图所示的数轴上，点B与点C关于点A对称，A，B两点对应的实数分别是 $\sqrt{2}$ 和﹣1，则点C所对应的实数是（）

A、 $1 + \sqrt{2}$ B、 $2 + \sqrt{2}$ C、 $2 \sqrt{2} - 1$ D、 $2 \sqrt{2} + 1$

查看试题解析
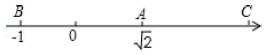12. 如图是一个按某种规律排列的数阵：根据数阵排列的规律，第n（n是整数，且n≥3）行从左向右数第（n﹣2）个数是（　　　）（用含n的代数式表示）

A、 $\sqrt{n^{2} - 1}$ B、 $\sqrt{n^{2} - 2}$ C、 $\sqrt{n^{2} - 3}$ D、 $\sqrt{n^{2} - 4}$

查看试题解析

二、填空题

13. $\sqrt{16}$ 的算术平方根是

查看试题解析
14. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
15. 若等腰三角形的周长是 $40 c m$ ，腰长 $y (c m)$ 是底边长 $x (c m)$ 的函数，则这个函数关系式是（ $0 < x < 20$ ）．

查看试题解析
16. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为 $8 c m$ ，正方形A的面积是 $11 c m$ ， B的面积是 $10 c m^{2}$ ， C的面积是 $13 c m^{2}$ ，则D的面积为．

查看试题解析
17. 若函数 $y = (k - 2) x^{| k - 1 |} + 1$ 是表示一次函数，则k等于．

查看试题解析
18. 在平面直角坐标系中，点 $A (1 ， 2 a + 3)$ 到x轴的的距离与到y轴的距离相等，则a= ．

查看试题解析

三、解答题

19. 计算： ${(\sqrt{2} - 1)}^{0} + | - 3 | - \sqrt[3]{27} + {(- 1)}^{2021}$ .

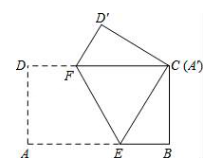
查看试题解析
20. 如图，将长AB=5cm，宽AD=3cm的长方形纸片ABCD折叠，使点A与C重合，折痕为EF，则AE长是多少？

查看试题解析
21. 为庆祝商都正式营业，商都推出了两种购物方案．方案一：非会员购物所有商品价格可获九五折优惠，方案二：如交纳300元会费成为该商都会员，则所有商品价格可获九折优惠．

(1)、以x（元）表示商品价格，y（元）表示支出金额，分别写出两种购物方案中y关于x的函数解析式；

(2)、若某人计划在商都购买价格为5880元的电视机一台，请分析选择哪种方案更省钱？

查看试题解析
22. 如图，正方形网格中的△ABC，若小方格边长为1，格点三角形（顶点是网格线交点的三角形）ABC的顶点A，C的坐标分别为（﹣1，1），（0，﹣2），请你根据所学的知识．
（ 1 ）在如图所示的网格平面内作出平面直角坐标系；
（ 2 ）作出三角形ABC关于y轴对称的三角形A₁B₁C₁；
（ 3 ）判断△ABC的形状，并求出△ABC的面积．

查看试题解析
23. 若实数y的立方根是2，且实数x、y、z满足 $\sqrt{x - 6} + y + (x - z + 4)^{2} = 8$ ，

(1)、求x+y﹣2z的值；

(2)、若x、y、z是△ABC的三边长，试判断△ABC的形状．

查看试题解析
24. 阅读下面式子： $\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1 ， \frac{1}{\sqrt{3} + \sqrt{2}}$ $= \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + 2) (\sqrt{3} - 2)} = \sqrt{3} - \sqrt{2} ， \frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ ．根据以上解法，试求：

(1)、 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （n为正整数）的值；

(2)、 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \cdot \cdot \cdot + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ 的值．

查看试题解析