山东省青岛市胶州市2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-27 类型:期中考试
一、单选题
-
1. 在综合实践活动课上,小明用三根木棒首尾顺次相接摆三角形.下列每组数分别是三根木棒的长度(单位:cm),其中能摆出直角三角形的一组是( )A、4,4,7 B、32,42,52 C、9,12,15 D、6,7,82. 如图,已知OA=OB,点A表示的数为a,则下列说法正确的是( )
 A、a的值为﹣3.1 B、a的绝对值为 C、a的相反数为3.1 D、a的倒数为3. 在平面直角坐标系内有一点P(x,y),已知x,y满足+|3y+5|=0,则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 近年来,作为规模较小的城市绿色敞开空间,口袋公园改善了城市生态环境,方便了市民健身休闲.如图,某口袋公园内有两条互相垂直的道路OA,OB,若OA长40m,OB长20m,当小明从A点沿公园内小路(图中箭头所示路线)走到B点时,小明所走的路程可能是( )
A、a的值为﹣3.1 B、a的绝对值为 C、a的相反数为3.1 D、a的倒数为3. 在平面直角坐标系内有一点P(x,y),已知x,y满足+|3y+5|=0,则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 近年来,作为规模较小的城市绿色敞开空间,口袋公园改善了城市生态环境,方便了市民健身休闲.如图,某口袋公园内有两条互相垂直的道路OA,OB,若OA长40m,OB长20m,当小明从A点沿公园内小路(图中箭头所示路线)走到B点时,小明所走的路程可能是( ) A、35m B、42m C、44m D、52m5. 从地面竖直向上抛射一个物体,经测量,在落地之前,物体向上的速度v(m/s)与运动时间t(s)之间有如下的对应关系,则速度v与时间t之间的函数关系式可能是( )
A、35m B、42m C、44m D、52m5. 从地面竖直向上抛射一个物体,经测量,在落地之前,物体向上的速度v(m/s)与运动时间t(s)之间有如下的对应关系,则速度v与时间t之间的函数关系式可能是( )v(m/s)
25
15
5
﹣5
t(s)
0
1
2
3
A、v=25t B、v=﹣10t+25 C、v=t2+25 D、v=5t+106. 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.若每个小立方块的体积为216cm³,则该几何体的最大高度是( )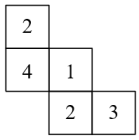 A、6cm B、12cm C、18cm D、24cm7. 若点A(﹣2,y1),点B(1,y2),点C(3,1)都在一次函数y=kx+7的图象上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定8. 在同一平面直角坐标系中,一次函数y=kx+b与正比例函数y=﹣x(k,b是常数,且kb≠0)的图象可能是( )A、
A、6cm B、12cm C、18cm D、24cm7. 若点A(﹣2,y1),点B(1,y2),点C(3,1)都在一次函数y=kx+7的图象上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定8. 在同一平面直角坐标系中,一次函数y=kx+b与正比例函数y=﹣x(k,b是常数,且kb≠0)的图象可能是( )A、 B、
B、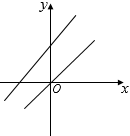 C、
C、 D、
D、
二、填空题
-
9. 下列各数3.14159,﹣ , , ﹣π,0, , 2.34010101…(相邻两个1之间有1个0)中,无理数有个.10. 若的平方根是±4,则a= .11. 将直线y=5x﹣1向下平移2个单位,可以得到一个一次函数的图象,则这个一次函数的表达式为 .12. 在平面直角坐标系中,点P在x轴的上侧,在y轴的左侧,距离每个坐标轴都是4个单位,则点P关于y轴的对称点P′的坐标为 .13. 比较大小: . (用“>”,“<”或“=”填空)14. 若一个等腰三角形的周长为16cm,一边长为6cm,则该等腰三角形的面积为cm215. 已知关于x的方程kx+b=0(k≠0)的解为x=﹣2,在一次函数y=kx+b(k≠0)图象中,当x每增加1个单位时,y增加了3个单位.若点P(5,y)为一次函数y=kx+b(k≠0)图象上一点,则点P到x轴的距离为 .16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(8,0),(8,6), , 点D为线段上一动点,将沿翻折,使点C落到点E处.当B,E两点之间距离最短时,点D的坐标为 .

三、解答题
-
17. 计算:(1)、(1+)(2﹣);(2)、(+)×;(3)、+3+;(4)、+ .18. 已知正数a的两个平方根分别是2x﹣3和1﹣x,且与互为相反数,求a+2b的值.19. 为了庆祝中国共产党成立100周年,某校组织了“请党放心,强国有我”党史知识竞赛,学校决定购买A,B两种奖品共120件,对表现优异的学生进行奖励.已知A种奖品的价格为32元/件,B种奖品的价格为15元/件.(1)、请直接写出购买两种奖品的总费用y(元)与购买A种奖品的数量x(件)之间的关系式;(2)、当购买了30件A种奖品时,总费用是多少元?(3)、若购买的A种奖品不多于50件,则总费用最多是多少元?20. 在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17,求△ABC的面积.
 21. A,B两地相距60km,甲乙两人沿同一条路从A地前往B地,甲先出发.图中l1 , l2表示甲乙两人离A地的距离y(km)与乙所用时间x(h)之间的关系,请结合图象回答下列问题:
21. A,B两地相距60km,甲乙两人沿同一条路从A地前往B地,甲先出发.图中l1 , l2表示甲乙两人离A地的距离y(km)与乙所用时间x(h)之间的关系,请结合图象回答下列问题:
 (1)、图中表示甲离A地的距离y(km)与乙所用时间x(h)之间关系的是(填l1或l2);(2)、当其中一人到达B地时,另一人距B地km;(3)、乙出发多长时间时,甲乙两人刚好相距10km?22. 如图,在正方形网格中,每个小正方形的边长均为1,图中四边形ABCD的每一个顶点都在格点上,请解答下列问题:
(1)、图中表示甲离A地的距离y(km)与乙所用时间x(h)之间关系的是(填l1或l2);(2)、当其中一人到达B地时,另一人距B地km;(3)、乙出发多长时间时,甲乙两人刚好相距10km?22. 如图,在正方形网格中,每个小正方形的边长均为1,图中四边形ABCD的每一个顶点都在格点上,请解答下列问题: (1)、画出以点A所在的横线为横轴,以点D所在的纵线为纵轴的直角坐标系;(2)、在(1)的直角坐标系中,写出点C关于x轴对称的点E的坐标;(3)、在(1)的直角坐标系中,求直线BD的函数关系式;(4)、求△ABD的面积.23. 问题提出:如图是某城市规划的“五横五纵”轨道交通示意图(每条线的交点代表一个站点),如果要想从站点A到站点B(只能按照从上往下,从左往右的方向行进),那么会有多少种不同的线路可以选择?
(1)、画出以点A所在的横线为横轴,以点D所在的纵线为纵轴的直角坐标系;(2)、在(1)的直角坐标系中,写出点C关于x轴对称的点E的坐标;(3)、在(1)的直角坐标系中,求直线BD的函数关系式;(4)、求△ABD的面积.23. 问题提出:如图是某城市规划的“五横五纵”轨道交通示意图(每条线的交点代表一个站点),如果要想从站点A到站点B(只能按照从上往下,从左往右的方向行进),那么会有多少种不同的线路可以选择?问题探究:为了解决问题,我们可以采用从特殊到一般的数学思想,先从最简单的情形入手,从中找到解决问题的方法.
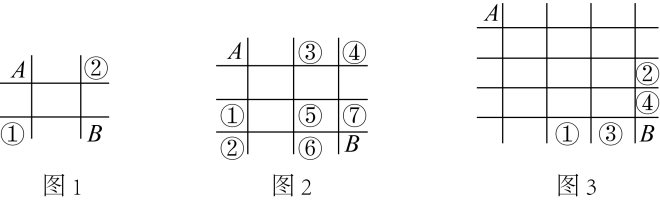
探究一:如果有“两横两纵”四条轨道,如图1所示要想从站点A到达站点B,要么先从上往下到站点①,要么先从左往右到站点②,而从站点A到达站点①,站点②的路线都只有一条,所以,从站点A到达站点B的路线数为到达站点①和站点②的路线数之和,即1+1=2条.探究二:如果有“三横三纵”六条轨道,如图2所示.要想从站点A到达站点B,必须先到达站点⑥或者站点⑦,所以为了探究从站点A到达站点B的路线数,我们可以先探究从站点A到达站点⑥和站点⑦的路线数,两者之和即为从站点A到达站点B的路线数.由探究一可知,从站点A到达站点⑤,有1+1=2条路线,从站点A直接到达站点②,只有1条路线,所以,从站点A到达站点⑥共有1+2=3条路线;从站点A直接到达站点④,也只有1条路线,所以,从站点A到达站点⑦共有1+2=3条路线,因此,从站点A到达站点B共有3+3=6条路线.
探究三:如果有“四横四纵”八条轨道,如图3所示.要想从站点A到达站点B,请仿照上面的探究过程,完成下表:
问题解决:在“五横五纵”轨道交通中,要想从站点A到站点B(只能按照从上往下,从左往右的方向行进),那么会有种不同的线路可以选择.站点
①
②
③
④
B
路线数
24. 如图,在Rt△ABC中,AC=3cm,BC=4cm,AB=5cm.动点E从点A出发,沿AB方向以1cm/s的速度向点B运动,同时动点F从点B出发,沿BC方向以1cm/s的速度向点C运动,连接CE,EF.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t(s)(0<t<4),请解答下列问题: (1)、当CE⊥AB时,求t的值;(2)、是否存在某一时刻t,使CE=CF,若存在,求出t的值;若不存在,请说明理由;(3)、设四边形AEFC的面积为ycm2 , 求y与t之间的关系式.
(1)、当CE⊥AB时,求t的值;(2)、是否存在某一时刻t,使CE=CF,若存在,求出t的值;若不存在,请说明理由;(3)、设四边形AEFC的面积为ycm2 , 求y与t之间的关系式.