山东省青岛市城阳区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-27 类型:期中考试
一、单选题
-
1. 的平方根是( )A、4 B、-4 C、±4 D、±22. 下列各数: , , , ﹣3,2.050050005…(相邻两个5之间的0的个数逐次加1),其中无理数有( )A、1个 B、2个 C、3个 D、4个3. 在平面直角坐标系中,点M(-3,1)在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 以下列各组数为边长,不能构成直角三角形的是( )A、3,4,5 B、 , , C、1.5,2,3 D、9,12,155. 下列运算正确的是( )A、﹣= B、= C、=2 D、﹣=26. 下列说法错误的是( )A、0的平方根是0 B、一个负数的立方根是一个负数 C、﹣8的立方根是﹣2 D、8的算术平方根是27. 已知正比例函数y=kx的图象如图所示,则一次函数y=kx﹣k的图象是( )
 A、
A、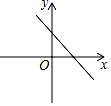 B、
B、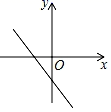 C、
C、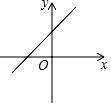 D、
D、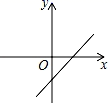 8. 如图,斜坡BC的长度为4米.为了安全,决定降低坡度,将点C沿水平距离向外移动4米到点A,使得斜坡AB的长度为4米,则原来斜坡的水平距离CD的长度是( )米.
8. 如图,斜坡BC的长度为4米.为了安全,决定降低坡度,将点C沿水平距离向外移动4米到点A,使得斜坡AB的长度为4米,则原来斜坡的水平距离CD的长度是( )米. A、2 B、4 C、2 D、6
A、2 B、4 C、2 D、6二、填空题
-
9. 10-3的立方根是 .10. 如果P(m+5,2m+4)在x轴上,那么点P的坐标是 .11. 已知点A(x,4)与B(﹣3,y)关于x轴对称,则2y﹣x= .12. 已知一个三角形的三边长分别为cm、3cm、2cm,则这个三角形的面积为cm2 .13. 如图,在△ABC中,∠C=90°,AC=12cm,BC=16cm,D、E分别是边BC、AB上的任意一点,把△ABC沿着直线DE折叠,顶点B的对应点是B′,如果点B′和顶点A重合,则CD=cm.
 14. 已知(﹣2,y1),(﹣1.5,y2),(1,y3)是直线y=﹣3x+b(b为常数)上的三个点,则y1、y2、y3的大小关系是 . (用“>”表示)15. 已知直线y=3x与y=﹣x+b的交点坐标为(a,3)则2b+a的平方根是 .16. 十一月的中山公园菊花盛开,甲乙两人约定去中山公园游玩,甲开汽车,乙骑摩托车分别从A、B两地同时沿同一路线去中山公园,他们距离A地的路程y(km)随时间x(h)变化的图象如图所示,已知甲开汽车离A地的路程y(km)与行驶时间x(h)满足y=50x,甲乙行驶h,两人第一次相遇.
14. 已知(﹣2,y1),(﹣1.5,y2),(1,y3)是直线y=﹣3x+b(b为常数)上的三个点,则y1、y2、y3的大小关系是 . (用“>”表示)15. 已知直线y=3x与y=﹣x+b的交点坐标为(a,3)则2b+a的平方根是 .16. 十一月的中山公园菊花盛开,甲乙两人约定去中山公园游玩,甲开汽车,乙骑摩托车分别从A、B两地同时沿同一路线去中山公园,他们距离A地的路程y(km)随时间x(h)变化的图象如图所示,已知甲开汽车离A地的路程y(km)与行驶时间x(h)满足y=50x,甲乙行驶h,两人第一次相遇.
三、解答题
-
17. 如图,在边长为1的正方形网格中,等边三角形ABC的顶点A、B、C的坐标分别是A(﹣2,0),B(4,0),C(m,n)且mn>0,求:
 (1)、写出边BC的长;(2)、在如图所示的网格平面内建立适当的直角坐标系;(3)、写出点C的坐标.18. 计算:(1)、 .(2)、 .(3)、()×﹣6 .(4)、﹣3+ .19. 如图,小东将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约4米,请算出旗杆的高度.
(1)、写出边BC的长;(2)、在如图所示的网格平面内建立适当的直角坐标系;(3)、写出点C的坐标.18. 计算:(1)、 .(2)、 .(3)、()×﹣6 .(4)、﹣3+ .19. 如图,小东将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约4米,请算出旗杆的高度.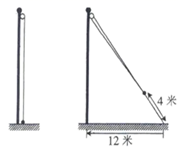 20. 生态兴则文明兴,生态衰则文明衰.“十三五”以来,青岛市坚持生态优先、绿色发展理念,持续改善生态环境.如图现有施工遗留的一处空地,计划改造成绿地公园,已知∠A=90°,AB=AD=3米,BC=10米,CD=8米,已知每平方米的改造费用为200元,请问改造该区域需要花费多少元?
20. 生态兴则文明兴,生态衰则文明衰.“十三五”以来,青岛市坚持生态优先、绿色发展理念,持续改善生态环境.如图现有施工遗留的一处空地,计划改造成绿地公园,已知∠A=90°,AB=AD=3米,BC=10米,CD=8米,已知每平方米的改造费用为200元,请问改造该区域需要花费多少元? 21. 已知:A、B都是x轴上的点,点A的坐标是(3,0),且线段AB的长等于4,点C的坐标是(0,2).
21. 已知:A、B都是x轴上的点,点A的坐标是(3,0),且线段AB的长等于4,点C的坐标是(0,2). (1)、直接写出点B的坐标.(2)、求直线BC的函数表达式.22. 我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,某地地面温度为30℃,设高出地面x千米处的温度为y℃.(1)、写出y与x之间的函数关系式.(2)、已知该地一座山峰高出地面约2500米,求这时山顶的温度大约是多少℃?(3)、此刻,有一架飞机飞过该地上空,若机舱内仪表显示飞机外面的温度为﹣36℃,求飞机离地的高度是多少千米?23. [阅读材料]
(1)、直接写出点B的坐标.(2)、求直线BC的函数表达式.22. 我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,某地地面温度为30℃,设高出地面x千米处的温度为y℃.(1)、写出y与x之间的函数关系式.(2)、已知该地一座山峰高出地面约2500米,求这时山顶的温度大约是多少℃?(3)、此刻,有一架飞机飞过该地上空,若机舱内仪表显示飞机外面的温度为﹣36℃,求飞机离地的高度是多少千米?23. [阅读材料]我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,为三角形和多边形的面积计算提供了新的方法和思路,在知道三角形三边的长而不知道高的情况下使用秦九韶公式可以更简便地求出面积,比如说在测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地求出答案,即三角形的三边长分别为a、b、c,则其面积S=(秦九韶公式),此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a、b、c,记p= , 则其面积S=(海伦公式),虽然这两个公式形式上有所不同,但它们本质是等价的,计算各有优劣,它填补了中国数学史中的一个空白,从中可以看出中国古代已经具有很高的数学水平.
[解决问题]
(1)、当三角形的三边a=7,b=8,c=9时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.(2)、当三角形的三边a= , b=2 , c=3时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.24. [学习探究]
[学习探究]数学中,常对同一图形的面积用两种不同的方法计算,从而建立相等关系,这是一种重要的数学方法.如图1,两个直角边分别为a、b、斜边长为c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形.
解:有三个直角三角形其面积分别为ab,ab和c2 ,
直角梯形的面积为(a+b)(a+b).
由图形可知:(a+b)(a+b)=ab+ab+c2 .
整理得(a+b)2=2ab+c2 , a2+b2+2ab=c2+2ab.
∴a2+b2=c2 .
故结论为:直角边长分别为a、b斜边为c的直角三角形中a2+b2=c2 .
(1)、[类比尝试]如图2,已知Rt△ABC中,∠ACB=90°,BC=5,AB=13,点D是AB上一动点,求CD的最小值是多少?
(2)、如图3,在4×4的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,若BD是△ABC的边AC上的高,求:①△ABC的面积;
②BD的长.
(3)、[拓展探究]如图4,在平面直角坐标系中,直线l1:y=x+10与x轴、y轴分别交于点A和B,直线l2经过坐标原点,且l2⊥l1 , 垂足为C,求:
①写出A点和B点的坐标.
②点C到x轴的距离.