山东省临沂市沂南县2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列科学防控“新冠肺炎”的图片中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 点 $A (3 ， 2)$ 与点Q关于y轴对称，则点Q的坐标为（）

A、 $(- 3 ， 2)$ B、 $(- 3 ， - 2)$ C、 $(3 ， - 2)$ D、 $(2 ， 3)$

查看试题解析
3. 已知三角形的一边长为8，则它的另两边长分别可以是（）

A、2，9 B、17，29 C、3，12 D、4，4

查看试题解析
4. 如图，小明在院子的门板上钉了一个加固板，从数学角度看，这样做的原因是（）

A、两点之间的线段最短 B、长方形的四个角都是直角 C、长方形具有稳定性 D、三角形有稳定性

查看试题解析
5. 已知，图中的虚线部分是小玉作的辅助线，则下列结论正确的是（）

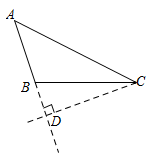A、CD是边AB上的高 B、CD是边AC上的高 C、BD是边CB上的高 D、BD是边AC上的高

查看试题解析
6. 已知 $△ A B C$ 的三个内角的大小关系为 $∠ A - ∠ B = ∠ C$ ，则这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
7. 如图， $△ A B E ≌ △ A C D$ ，则与 $∠ B$ 相等的是（）

A、 $∠ C A D$ B、 $∠ A E D$ C、 $∠ C$ D、 $∠ C A E$

查看试题解析
8. 根据下列图中所给定的条件，找出全等的三角形（）

A、①和② B、②和③ C、①和③ D、①和④

查看试题解析
9. 若n边形每个内角都为156°，那么n等于（）

A、8 B、12 C、15 D、16

查看试题解析
10. 如图，DE是△ABC的边BC的垂直平分线，分别交边AB，BC于点D，E，且AB＝9，AC＝6，则△ACD的周长是（）

A、10.5 B、12 C、15 D、18

查看试题解析
11. 如图， $△ A B C$ 为等边三角形，BO为中线，延长BA至D，使 $A D = A O$ ，则 $∠ D O B$ 的度数为（）

A、 $105 °$ B、 $120 °$ C、 $135 °$ D、 $150 °$

查看试题解析
12. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形PCQD是一个筝形，其中 $P C = P D$ ， $C Q = D Q$ ，在探究筝形的性质时，得到如下结论：① $△ P C Q ≌ △ P D Q$ ；② $P Q ⊥ C D$ ；③ $C E = D E$ ；④ $S_{四边形 P C Q D} = \frac{1}{2} P Q \cdot C D$ ，其中正确的结论有（）

A、①② B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题

13. 如图， $A B ∥ C D$ ，点E在AD上，且 $D C = D E$ ， $∠ C = 70 °$ ，则 $∠ A$ 的大小为．

查看试题解析
14. 六边形的内角和比它的外角和多度．

查看试题解析
15. 如图，点F，A，D，C在同一条直线上， $△ A B C ≌ △ D E F$ ， $A D = 3$ ， $C F = 10$ ，则AC等于．

查看试题解析
16. 如图，四边形ABCD中， $∠ A = 90 °$ ， $A D = 3$ ，连接BD， $B D ⊥ C D$ ，垂足为D， $∠ A D B = ∠ C$ ，点P是边BC上的一动点，则DP的最小值是．

查看试题解析
17. 如图，在△ABC中， $∠ C = 90 °$ ， AD平分 $∠ C A B$ ，交BC于点D，若 $∠ A D C = 60 °$ ， $C D = 2$ ，则BC的长度等于．

查看试题解析
18. 如图， $C A ⊥ A B$ ，垂足为点A ，射线 $B M ⊥ A B$ ，垂足为点B ， $A B = 12 cm$ ， $A C = 6 cm$ ．动点E从A点出发以3cm/s的速度沿射线AN运动，动点D在射线BM上，随着 E点运动而运动，始终保持 $E D = C B$ ．若点E的运动时间为 $t (t > 0)$ ，则当 $t =$ 个秒时， $△ D E B$ 与 $△ B C A$ 全等．

查看试题解析

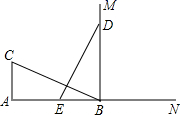
三、解答题

19. 如图， $A D ⊥ B C$ ，垂足为D，点E在AC上， $∠ A = 32 °$ ， $∠ B = 40 °$ ．求 $∠ A E F$ 的度数．

查看试题解析
20. △ABC在平面直角坐标系的位置如图所示（注：图中每小正方形的边长均为1）

(1)、请画出△ABC关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ （ $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 分别是A、B、C的对应点，不写画法）；

(2)、直接写出 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 三点的坐标：、、．

(3)、△ABC的面积是．

查看试题解析
21. 如图，已知AC，BD相交于点O， $B C = A D$ ， $A C = B D$ ．求证： $∠ D = ∠ C$ ．

查看试题解析
22. 如图，A、B两村位于两条公路m、n之间，为响应“建设新农村”号召，两村决定在S区联合修建一所配套设施完善的卫生室C，卫生室到两村的距离相等，且到两条公路的距离相等．请你按要求确定出C的位置（尺规作图，保留作图痕迹，不写作法）：

查看试题解析
23. 如图，△ABC是等边三角形，BD平分∠ABC交AC于点D，过点D作 $E F ⊥ A B$ 于E，交BC边延长线于F，若 $A E = 2$ ，求BF的长．

查看试题解析
24. 如图，在△ABC中，AB的垂直平分线MN交AB于点D，交AC于点E，且 $A C = 15 c m$ ， △BCE的周长等于 $24 c m$ ．

(1)、求BC的长；

(2)、若 $∠ A = 36 °$ ，并且 $A B = A C$ ．求证： $B C = B E$ ．

查看试题解析
25. 如图，在等腰Rt△ABC中， $∠ A C B = 90 °$ ， D为BC的中点， $D E ⊥ A B$ ，垂足为E，过点B作 $B F ∥ A C$ ，交DE的延长线于点F，连接CF．

(1)、求证： $A D = C F$ ；

(2)、连接AF，试判断△ACF的形状，并说明理由．

查看试题解析