山东省济宁市任城区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，是分式的是（）

A、 $x$ B、 $\frac{x}{x + 2}$ C、 $\frac{x}{π}$ D、 $\frac{x}{2} + 1$

查看试题解析
2. 若分式 $\frac{x}{x + 1}$ 有意义，则x的取值范围是（　　）

A、x≠﹣1 B、x≠1 C、x＝﹣1 D、x＝1

查看试题解析
3. 下列等式从左到右的变形，属于因式分解的是（）

A、 $a (x - y) = a x - a y$ B、 $x^{2} + 2 x + 1 = x (x + 2) + 1$ C、 $(x + 1) (x + 3) = x^{2} + 4 x + 3$ D、 $x^{3} - x = x (x + 1) (x - 1)$

查看试题解析
4. 山茶花是温州市的市花、品种多样，“金心大红”是其中的一种，某兴趣小组对30株“金心大红”的花径进行测量、记录，统计如下表。

株数(株)

7

9

12

2

花径(cm)

6.5

6.6

6.7

6.8

这批“金心大红”花径的众数为（）

A、6.5cm B、6.6cm C、6.7cm D、6.8cm

查看试题解析
5. 化简 $\frac{a^{2} - 2 a}{2 - a}$ 的结果是（）

A、﹣1 B、1 C、﹣a D、a

查看试题解析
6. 下列各式中，哪项可以使用平方差公式分解因式（）

A、 $- a^{2} - b^{2}$ B、 $- a^{2} + 9$ C、 $p^{2} - (- q^{2})$ D、 $a^{2} - b^{3}$

查看试题解析
7. 如果 $\frac{a + b}{3 a} = \frac{1}{2}$ ，那么 $\frac{b}{a}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{5}$

查看试题解析
8. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数x（单位：千克）及方差S²（单位：千克²）如下表所示：

甲

乙

丙

丁

x

24

24

23

20

S²

2.1

1.9

2

1.9

今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 某工程队在忠州街道改造一条长 $6000$ 米的人行步道，为尽量减少施工对交通造成的影响，施工时“×××”，设实际每天改造人行步道 $x$ 米，则可得方程 $\frac{6000}{x - 18} = \frac{6000}{x} + 25$ ，根据已信息，题中用“×××”表示的缺失的条件应补为（）

A、每天比原计划多铺设18米，结果提前25天完成 B、每天比原计划多铺设18米，结果延期25天完成 C、每天比原计划少铺设18米，结果延期25天完成 D、每天比原计划少铺设18米，结果提前25天完成

查看试题解析
10. 如图，设 $k = \frac{甲图中阴影部分面积}{乙图中阴影部分面积} (a > b > 0)$ ，则k的值可以为（）

A、 $\frac{1}{2}$ B、 $1$ C、 $\frac{3}{2}$ D、 $2$

查看试题解析

二、填空题

11. 单项式4m²n²与12m³n²的公因式是．

查看试题解析
12. 5月1日至7日，某市每日最高气温如图所示，则中位数是．

查看试题解析
13. 若多项式 $x^{2} + m x + 25$ 能用完全平方公式因式分解，则m的值为．

查看试题解析
14. 分解因式x²+3x+2的过程，可以用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数（如右图）.这样，我们可以得到x²+3x+2＝（x+1）（x+2）.请利用这种方法，分解因式2x²﹣3x﹣2＝.

查看试题解析

三、解答题

15. 已知 $x - y = 2 ， \frac{1}{x} - \frac{1}{y} = 1$ ，求 $x^{2} y - x y^{2}$ 的值.

查看试题解析
16. 分解因式：

(1)、 $x^{3} - 25 x$ ；

(2)、 $m (a - 3) + 2 (3 - a)$ ．

查看试题解析
17. 计算：

(1)、4a²b÷（﹣ $\frac{2 a}{b}$ ）² ．

(2)、 $\frac{a^{2}}{a - b} + \frac{b^{2}}{b - a}$ ．

查看试题解析
18. 解分式方程：

(1)、 $\frac{2}{x} - \frac{3}{x - 1} = 0$ ；

(2)、 $\frac{1 - x}{2 - x} = \frac{1}{x - 2} + 3$ ．

查看试题解析
19. 为了了解某校八年级学生每周平均课外阅读时间的情况，随机抽取了50名八年级学生，对其每周平均课外阅读时间进行统计，并绘制成下面的统计图。

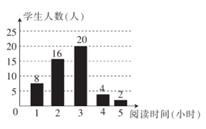(1)、这50名同学每周阅读时间的众数为小时，中位数为小时。

(2)、求出这组数据的平均数。

查看试题解析
20. 利用因式分解计算：

(1)、2²⁰¹⁴﹣2²⁰¹³；

(2)、（﹣2）¹⁰¹+（﹣2）¹⁰⁰ ．

查看试题解析
21. 先化简，再求值： $(\frac{1}{a - 3} + \frac{1}{a + 3}) \div \frac{2 a}{a^{2} - 6 a + 9}$ ，其中 $a = - 2$ ．

查看试题解析
22. 某公司对甲、乙两名应聘者进行面试，并按专业知识、工作经验和仪表形象三项给应聘者打分，每项满分20分，打分结果如下表（单位：分）：

专业知识
工作经验
仪表形象
甲
14
18
12
乙
18
16
11
根据实际需要，公司将专业知识、工作经验和仪表形象三项得分按6∶3∶1的比确定应聘者的最终成绩，那么应该录用谁？请说明理由．

查看试题解析
23. 对于任意实数a，b我们规定：a⊗b＝ ${\begin{array}{l} \frac{b}{4 a - b} ， (a \geq b) \\ \frac{a}{4 a + b} ， (a \leq b) \end{array}$ ．根据上述规定解决下列问题：

(1)、计算：（﹣ $\frac{1}{2}$ ）⊗（﹣1）．

(2)、若（x﹣3）⊗（x+3）＝1，求x的值．

查看试题解析
24. 近年来，雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置，需购进 $A ， B$ 两种设备.已知每台 $B$ 种设备比每台 $A$ 种设备价格多0.6万元，花5万元购买A种设备和花11万元购买B种设备的数量相同.

(1)、求 $A ， B$ 两种设备每台各多少万元.

(2)、根据单位实际情况，需购进 $A ， B$ 两种设备共18台，总费用不高于14万元.求 $A$ 种设备至少要购买多少台？

查看试题解析

株数(株)	7	9	12	2
花径(cm)	6.5	6.6	6.7	6.8

	甲	乙	丙	丁
x	24	24	23	20
S²	2.1	1.9	2	1.9

	专业知识	工作经验	仪表形象
甲	14	18	12
乙	18	16	11