山东省济宁市曲阜市、兖州区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2022-09-27 类型：期中考试
一、单选题
-
1. 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（ ）A、1 B、2 C、8 D、112. 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（ ）A、
B、
C、
D、
3. 下列图形具有稳定性的是（ ）A、
B、
C、
D、
4. 如图，在 中，AC边上的高是（ ）
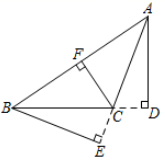A、BE B、AD C、CF D、AF5. 在平面直角坐标系xOy中，已知点A(2，﹣1)，则点A关于x轴的对称点的坐标是（ ）A、(2，1) B、(﹣2，1) C、(﹣2，﹣1) D、(﹣1，2)6. 如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，连接AE，若AE＝4，EC＝2，则BC的长是（ ）
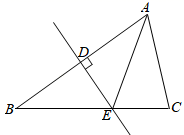A、2 B、4 C、6 D、87. 如图，在 的正方形网格中有两个格点A、B，连接 ，在网格中再找一个格点C，使得 是等腰直角三角形，满足条件的格点C的个数是（ ）
A、2 B、3 C、4 D、58. 如图，点A、B、C、D、E在同一平面内，连接 、 、 、 、 ，若 ，则 （ ）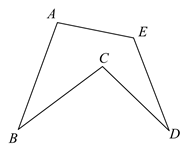
A、 B、 C、 D、9. 如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，若点A关于CD所在直线的对称点E恰好为AB的中点，则∠B的度数是（ ）
A、60° B、45° C、30° D、75°10. 如图，小球起始时位于 处，沿所示的方向击球，小球运动的轨迹如图所示.如果小球起始时位于 处，仍按原来方向击球，小球第一次碰到球桌边时，小球的位置是 ，那么小球第2020次碰到球桌边时，小球的位置是（ ）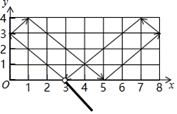
A、 B、 C、 D、二、填空题
-
11. 一副三角板按如图方式放置，含45°角的三角板的斜边与含30°角的三角板的长直角边平行，则∠α的度数是 ．
12. 一个多边形的每个外角都等于40°，则它的内角和是°．13. 如图所示的网格是正方形网格，△ABC的面积△DEF的面积．（填“＞”，“＝”或“＜”）．
14. 一个等腰三角形的两边长分别为5和3，则这个三角形的周长为.15. 如图所示，AB=AD，∠1=∠2，添加一个适当的条件，使△ABC≌△ADE，则需要添加的条件是.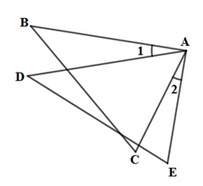
16. 如图，在中，和分别平分和 ， 过点作 ， 分别交于点 ， 若 ， 则线段的长为 ．
三、解答题
-
17. 如图所示，CD=CA，∠1=∠2，EC=BC，求证：△ABC≌△DEC．
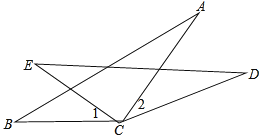18. 如图是A、B、C三岛的平面图，C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80°方向，C岛在B岛的北偏西40°方向．从C岛看A、B岛的视角∠ACB为多少？
19. 如图，在边长为1的正方形网格中有一个ABC，完成下列各图（用无刻度的直尺画图，保留作图痕迹）．
⑴作ABC关于直线MN对称的A1B1C1；
⑵求ABC的面积；
⑶在直线MN上找一点P，使得PA+PB最小．
20. 如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC．求证：DM=DN．
21. 已知：如图，线段AB和射线BM交于点B．
(1)、利用尺规完成以下作图，并保留作图痕迹（不写作法）①在射线BM上作一点C，使AC=AB，连接AC；
②作∠ABM 的角平分线交AC于D点；
③在射线CM上作一点E，使CE=CD，连接DE.
(2)、在（1）所作的图形中，猜想线段BD与DE的数量关系，并证明之．
