山东省济南市济阳区2021-2022学年八年级上学期期中考试数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 木工师傅想利用木条制作一个直角三角形，那么下列各组数据不符合直角三角形的三边长的是（）

A、3，4，5 B、6，8，10 C、5，12，13 D、7，15，17

查看试题解析
2. 在给出的一组数0， $π$ ， $\sqrt{5}$ ， 3.14， $\sqrt[3]{9}$ ， $\frac{22}{7}$ 中，无理数的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
3. 实数16的算术平方根是（　　）

A、8 B、±8 C、4 D、±4

查看试题解析
4. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{0.3}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{30}$ D、 $\sqrt{300}$

查看试题解析
5. 下列各式中，正确的是（）

A、 $\sqrt{8} \div \sqrt{2} = 2$ B、 $\sqrt{9} = \pm 3$ C、 $\sqrt{6} - \sqrt{2} = 2$ D、 $\sqrt{{(- 4)}^{2}} = - 4$

查看试题解析
6. 平面直角坐标系内，点 $P (- 2 ， 3)$ 到原点的距离是（）

A、2 B、3 C、 $\sqrt{13}$ D、2或3

查看试题解析
7. 如图，点A、B、C都在方格纸的格点上，若点A的坐标为(0，1)，点B的坐标为(2，−1)，则点C的坐标是（）

A、 $(2 ， 0)$ B、 $(0 ， 2)$ C、 $(- 2 ， 0)$ D、 $(0 ， - 2)$

查看试题解析
8. 一水池的容积是90m³ ，现有蓄水10m³ ，用水管以5m³/h的速度向水池注水，直到注满为止．则水池蓄水量V（m³）与注水时间t（h）之间的函数关系式为（）

A、 $V = 5 t$ B、 $V = 10 t$ C、V=10+5t D、 $V = 80 - 5 t$

查看试题解析
9. 如果直角三角形的两边长分别是3，4，那么斜边长是（）

A、5 B、 $\sqrt{7}$ C、5或 $\sqrt{7}$ D、5或4

查看试题解析
10. 对于一次函数y=x-4，下列结论错误的是（）

A、函数的图象与x轴的交点坐标是（0，-4） B、函数的图象不经过第二象限 C、函数的图象与坐标轴围成的三角形的面积为8 D、函数值随自变量的增大而增大

查看试题解析
11. 如图，已知钓鱼竿 $A C$ 的长为 $10 m$ ，露在水面上的鱼线 $B C$ 长为 $6 m$ ，某钓鱼者想看看鱼钩上的情况，把鱼竿 $A C$ 转动到 $A C^{'}$ 的位置，此时露在水面上的鱼线 $B^{'} C^{'}$ 为 $8 m$ ，则 $B B^{'}$ 的长为（）

A、 $1 m$ B、 $2 m$ C、 $3 m$ D、 $4 m$

查看试题解析
12. 如图1，在 $△ A B C$ 中， $A B = B C$ ， $B D ⊥ A C$ 于点 $D (A D > B D)$ ．动点M从A点出发，沿折线 $A B \to B C$ 方向运动，运动到点C停止．设点M的运动路程为x， $△ A M D$ 的面积为y，y与x的函数图象如图2，则AC的长为（）

A、4 B、6 C、8 D、10

查看试题解析

二、填空题

13. 在平面直角坐标系中，点（﹣2，1）在第象限．

查看试题解析
14. 化简： $3 \sqrt{2} + 2 \sqrt{2}$ ＝．

查看试题解析
15. 在平面直角坐标系中，将点M（3，－2）向下平移4个单位得到点N，则点N的坐标为．

查看试题解析
16. 如图，一座桥横跨一河，桥长40m，一艘小船自桥北头出发，向正南方驶去，因水流原因到达南岸后，发现已偏离桥南头9m，则小船实际行驶的距离为m．

查看试题解析
17. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的边长分别是2，3，1，2，则最大正方形E的面积是.

查看试题解析
18. 如图，一次函数y＝x＋2的图像与坐标轴分别交于A，B两点，点P，C分别是线段AB，OB上的点，且∠OPC＝45°，PC＝PO，则点P的坐标为．

查看试题解析

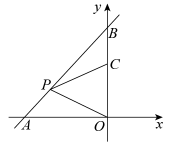
三、解答题

19. 计算：

(1)、 ${(\sqrt{2} + 1)}^{2} - \sqrt{8}$

(2)、 $(\sqrt{5} - \frac{1}{\sqrt{5}}) \times \sqrt{5}$

查看试题解析
20. 已知a的平方根是±3，b-1的算术平方根是2，求a-2b的立方根．

查看试题解析
21. 一住宅楼发生火灾，消防车立即赶到，准备在距大楼9米的C处升起云梯到火灾窗口展开营救，已知云梯AB长15m，云梯底部B距离地面2米，此时消防队员能否救下等候在距离地面约13米窗口的受困群众？说说你的理由．

查看试题解析
22. 漏刻是我国古代的一种计时工具．据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用．小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h（cm）是时间t（min）的一次函数，下表是小明记录的部分数据，其中有一个h的值记录不符合题意．
t（min）
0
1
2
3
5
…
h（cm）
2
2.4
2.8
3.4
4
…

(1)、错误的h的值是cm；

(2)、求水位h（cm）与时间t（min）的一次函数关系式；

(3)、当h为10cm时，对应的时间t为min．

查看试题解析
23. 观察下列一组等式，解答后面的问题：
$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) \times (\sqrt{3} - 1)} = \sqrt{3} - 1$
$\frac{2}{\sqrt{5} + \sqrt{3}} = \frac{2 \times (\sqrt{5} - \sqrt{3})}{(\sqrt{5} + \sqrt{3}) \times (\sqrt{5} - \sqrt{3})} = \sqrt{5} - \sqrt{3}$

(1)、化简： $\frac{2}{\sqrt{7} + \sqrt{5}} =$ ， $\frac{2}{\sqrt{n + 2} + \sqrt{n}} =$ （n为正整数）

(2)、比较大小： $\sqrt{21} - \sqrt{19}$ $\sqrt{19} - \sqrt{17}$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）

(3)、根据上面的结论，找规律，请直接写出下列算式的结果： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \cdot \cdot \cdot + \frac{1}{\sqrt{2021} + \sqrt{2019}} =$

查看试题解析
24. 如图，方格纸中的每个小方格的边长都是1，四边形ABCD的四个顶点都在格点上，A（-3，4），B（-4，1），C（-3，0）．

(1)、点D的坐标为．

(2)、在图中作出四边形ABCD关于y轴对称的四边形A₁B₁C₁D₁；

(3)、点E是x轴上的一个动点，当△OAE为等腰三角形时，请直接写出所有满足条件的点E的坐标．

查看试题解析
25. 甲超市在国庆节期间进行苹果优惠促销活动，苹果的标价为5元/kg，如果一次购买4kg以上的苹果，超过4kg的部分按标价6折售卖．其中x（单位：kg）表示购买苹果的重量， $y_{甲}$ （单位：元）表示付款金额．

(1)、文文购买3kg苹果需付款元；购买5kg苹果需付款元；

(2)、写出付款金额 $y_{甲}$ 关于购买苹果的重量x的函数关系式：

(3)、乙超市也在进行苹果优惠促销活动，同样的苹果的标价也为5元/kg，且全部按标价的8折售卖．文文如果要购买10kg苹果，请问她在哪个超市购买更划算？

查看试题解析
26. 甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示：

(1)、分别求甲车从A地到达B地的行驶过程中 $y_{甲}$ 与x之间的函数关系式和乙车从B地到达A地的行驶过程中 $y_{乙}$ 与x之间的函数关系式；

(2)、甲车到达B地的行驶时间为小时，甲车返回A地时的速度为千米/时，乙车行驶的速度为千米/时；

(3)、乙车到达A地时甲车距A地的路程为千米．

查看试题解析
27. 如图，在平面直角坐标系中，一次函数 $y = - \frac{1}{2} x + m$ 的图象 $l_{1}$ 分别与x，y轴交于A，B两点，正比例函数的图象 $l_{2}$ 与 $l_{1}$ 交于点 $C (2 ， 4)$ ．

(1)、求m的值及 $l_{2}$ 的解析式；

(2)、若点M是直线 $y = - \frac{1}{2} x + m$ 上的一个动点，连接OM，当 $△ A O M$ 的面积是 $△ B O C$ 面积的2倍时，请求出符合条件的点M的坐标；

(3)、一次函数 $y = k x + 2$ 的图象为 $l_{3}$ ，且 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 不能围成三角形，直接写出k的值．

查看试题解析

t（min）	0	1	2	3	5	…
h（cm）	2	2.4	2.8	3.4	4	…