山东省德州市德州经济技术开发区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 新型冠状病毒引发肺炎疫情，德州多家医院选派医护人员驰援武汉，如图是四家医院标志的图案部分，其中是轴对称图形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下面四个图形中，线段 $B D$ 是 $Δ A B C$ 的高的是（）

A、 B、 C、 D、

查看试题解析
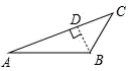3. 已知图中的两个三角形全等，则∠ $α$ 等于（）

A、 $7 2^{∘}$ B、 $6 0^{∘}$ C、 $5 8^{∘}$ D、 $5 0^{∘}$

查看试题解析
4. 如图，在 $Δ A B C$ 中，已知 $∠ A B C$ 和 $∠ A C B$ 的平分线相交于点F．过点F作 $D F ∥ B C$ ，交 $A B$ 于点D，交 $A C$ 于点E．若 $B D = 4$ ， $D E = 9$ ，则线段 $C E$ 的长为（）

A、3 B、4 C、5 D、6

查看试题解析
5. 多边形每一个内角都等于150°，则从该多边形一个顶点出发，可引出对角线的条数为（）

A、6条 B、8条 C、9条 D、12条

查看试题解析
6. 如果，在 $△ A B C$ 中， $∠ B = 38 °$ ， $∠ C = 54 °$ ， $A E$ 是 $B C$ 边上的高， $A D$ 是 $∠ B A C$ 的平分线，则 $∠ D A E$ 的度数为（）

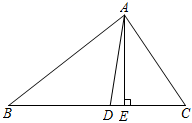A、8° B、10° C、12° D、14°

查看试题解析
7. 工人师傅常用角尺平分一个任意角．作法如下：如图所示，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC即是∠AOB的平分线．这种作法的道理是（）

A、HL B、SSS C、SAS D、ASA

查看试题解析
8. 如图，△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P，若点P到直线AC的距离为4，则点P到直线AB的距离为（　）

A、4 B、3 C、2 D、1

查看试题解析
9. 如图所示， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E$ ， $∠ 1 = 2 5^{∘}$ ， $∠ 2 = 3 0^{∘}$ ，则 $∠ 3 =$ （）

A、 $6 0^{∘}$ B、 $5 5^{∘}$ C、 $5 0^{∘}$ D、无法计算

查看试题解析
10. 如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果P也是图中的格点，且使得△ABP为等腰三角形，则点P的个数是（）

A、5 B、6 C、7 D、8

查看试题解析
11. 如图，已知 $Δ A B C$ 中， $A B = A C = 24 c m$ ， $∠ B = ∠ C$ ， $B C = 16 c m$ ，点D为 $A B$ 的中点，如果点P在线段 $B C$ 上以 $4 c m / s$ 的速度由B点向C点运动，同时，点Q在线段 $C A$ 上由C点向A点运动，当点Q的运动速度为（） $c m / s$ 时，能够在某一时刻使 $Δ B P D$ 与 $Δ C Q P$ 全等．

A、4 B、3 C、4或3 D、4或6

查看试题解析
12. 如图， $A$ ， $B$ ， $E$ 三点在同一直线上， $△ A B C$ ， $△ C D E$ 都是等边三角形，连接 $A D$ ， $B E$ ， $O C$ ：下列结论中正确的是（）
①△ACD≌△BCE；②△CPQ是等边三角形；③ $O C$ 平分 $∠ A O E$ ；④△BPO≌△EDO.

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

13. 等腰 $Δ A B C$ 的两边长分别为5，9，则这个等腰三角形的周长为．

查看试题解析
14. 若点P(-3，4)和点Q（a，b）关于 $x$ 轴对称，则2a+b=.

查看试题解析
15. 如图， $∠ A = 50 °$ ， $∠ A B O = 25 °$ ， $∠ A C O = 20 °$ ，求 $∠ B O C =$ ．

查看试题解析
16. 如图，点E，F在BC上，BE＝CF，∠A＝∠D．请添加一个条件，使△ABF≌△DCE

查看试题解析
17. 如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是°．

查看试题解析
18. 如图，已知 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 9 0^{∘}$ ，直角 $∠ E P F$ 的顶点P是 $B C$ 中点，两边 $P E$ 、 $P F$ 分别交 $A B$ 、 $A C$ 于点E、F，给出以下四个结论：① $A E = C F$ ；② $Δ E P F$ 是等腰直角三角形：③ $2 S_{四边形 A E P F} = S_{Δ A B C}$ ；④ $B E + C F = E F$ ．其中正确的有．（填序号）

查看试题解析

三、解答题

19. 如图，在 $Δ A B C$ 中， $B D$ 是 $∠ A B C$ 的角平分线， $D E ∥ B C$ ，交 $A B$ 于点E， $∠ A = 6 0^{∘}$ ， $∠ B D C = 9 5^{∘}$ ，求 $∠ E D B$ 的度数．

查看试题解析
20. 如图，电信部门要在S区修建一座发射塔P．按照设计要求，发射塔P到两个城镇A、B的距离必须相等，到两条高速公路m和n的距离也必须相等，发射塔P应建在什么位置？在图上标出它的位置．（尺规作图：只保留作图痕迹，不写作图过程）

查看试题解析
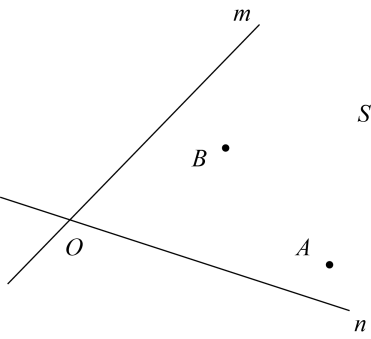21. 证明：如果两个三角形有两条边和其中一条边上的高分别相等，那么这两个三角形全等．请根据图形，用符号语言表示出已知和求证，并写出证明过程．

查看试题解析
22. 如图， $Δ A B C$ 中， $∠ C = 9 0^{∘}$ ．

(1)、求作 $Δ A E B$ ，使 $Δ A E B$ 是以 $A B$ 为底的等腰三角形，且使点E在边 $B C$ 上．要求：尺规作图，不写作法，保留作图痕迹．

(2)、在（1）所作的图形中，若 $∠ C A E ： ∠ E A B = 4 ： 1$ ．求证： $B E = 2 A C$ ．

查看试题解析
23. 如图， $C D ⊥ A B$ ， $B E ⊥ A C$ ，垂足分别为D、E， $B E$ 、 $C D$ 相交于点F， $A F$ 平分 $∠ B A C$ ．

(1)、求证： $B F = C F$ ；

(2)、连接 $B C$ ，试判断 $A F$ 与 $B C$ 的位置关系，并说明理由．

查看试题解析
24. 如图， $Δ A B C$ 在平面直角坐标系中，点A，B，C的坐标分别为 $A (2 ， 4)$ ， $B (- 5 ， 1)$ ， $C (- 1 ， - 2)$ ．

( 1 )画出 $Δ A B C$ 关于y轴成轴对称图形的 $Δ A^{'} B^{'} C^{'}$ ；

( 2 )在x轴上是否存在点P，使由P、A、 $B^{'}$ 构成的 $Δ A B^{'} P$ 的周长最小？若存在，标出点P的位置；若不存在，说明理由．

( 3 )点C关于直线l（直线l上各点的纵坐标都是 $- 3$ ）对称的点E的坐标是；点 $M (m ， n)$ 关于此直线l的对称点 $M^{'}$ 的坐标是．

查看试题解析
25. 数学课上，老师出示了如下框中的题目：

在等边三角形 $A B C$ 中，点E在 $A B$ 上，点D在 $C B$ 的延长线上，且 $E D = E C$ ，

如图，试确定线段 $A E$ 与 $D B$ 的大小关系，并说明理由．

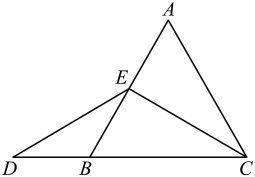
小敏与同桌小聪讨论后，进行了如下解答：

(1)、特殊情况，探索结论
当点E为 $A B$ 的中点时，如图1，确定线段 $A E$ 与 $D B$ 的大小关系．请你直接写出结论： $A E$ $D B$ （填“＞”，“＜”或“=”）．

(2)、特例启发，解答题目
解：题目中， $A E$ 与 $D B$ 的大小关系是： $A E$ $D B$ （填“＞”，“＜”或“=”）理由如下：

如图2，过点E作 $E F ∥ B C$ ，交 $A C$ 于点F，（请你继续完成解答过程）

(3)、拓展结论，设计新题
在等边三角形 $A B C$ 中，点E在直线上 $A B$ 上，点D在直线 $B C$ 上，且 $E D = E C$ ．若 $Δ A B C$ 的边长为3， $A E = 5$ ，求 $C D$ 的长（请你直接写出结果）．

查看试题解析