重庆110中2022-2023学年九年级上学期入学数学试卷
试卷更新日期:2022-09-27 类型:开学考试
一、选择题(本大题共12小题,共48分。)
-
1. 道路千万条,安全第一条,以下是一些常见的交通标识,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式 , 在数轴上可表示为( )A、
2. 不等式 , 在数轴上可表示为( )A、 B、
B、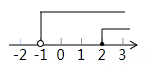 C、
C、 D、
D、 3. 下列各式中,能用平方差公式分解因式的是( )A、 B、 C、 D、4. 当x=3时,分式 没有意义,则b的值为( )A、-3 B、 C、 D、35. 如图,在中, , 垂直平分线交于点 , 交于点 , 的周长为17,则为( )
3. 下列各式中,能用平方差公式分解因式的是( )A、 B、 C、 D、4. 当x=3时,分式 没有意义,则b的值为( )A、-3 B、 C、 D、35. 如图,在中, , 垂直平分线交于点 , 交于点 , 的周长为17,则为( ) A、9 B、8 C、12 D、116. 如图,为了测量池塘边、两地之间的距离,在线段的同侧取一点 , 连结并延长至点 , 连结并延长至点 , 使得、分别是、的中点,若 , 则线段的长度是( )
A、9 B、8 C、12 D、116. 如图,为了测量池塘边、两地之间的距离,在线段的同侧取一点 , 连结并延长至点 , 连结并延长至点 , 使得、分别是、的中点,若 , 则线段的长度是( ) A、 B、 C、 D、7. 如图,在平面直角坐标系中,已知点 , , 以点为圆心,长为半径画弧,交轴的正半轴于点,则点的坐标是( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,已知点 , , 以点为圆心,长为半径画弧,交轴的正半轴于点,则点的坐标是( ) A、 B、 C、 D、8. 如下图,边长为、的长方形周长为16,面积为12,则的值为( )
A、 B、 C、 D、8. 如下图,边长为、的长方形周长为16,面积为12,则的值为( )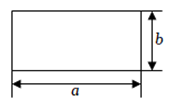 A、28 B、96 C、192 D、2009. 若关于的分式方程有增根,则的值为( )A、1 B、2 C、3 D、410. 如图,在平行四边形中, , 、分别在和的延长线上, , , 则的长为( )
A、28 B、96 C、192 D、2009. 若关于的分式方程有增根,则的值为( )A、1 B、2 C、3 D、410. 如图,在平行四边形中, , 、分别在和的延长线上, , , 则的长为( ) A、 B、 C、4 D、11. 若关于的分式方程的解为非负数,且关于的不等式组有3个整数解,则所有满足条件的整数的值之和为( )A、19 B、22 C、30 D、3312. 已知关于 , 的方程组 , 以下结论正确的有个.( )
A、 B、 C、4 D、11. 若关于的分式方程的解为非负数,且关于的不等式组有3个整数解,则所有满足条件的整数的值之和为( )A、19 B、22 C、30 D、3312. 已知关于 , 的方程组 , 以下结论正确的有个.( )①不论取什么实数,的值始终不变;②存在实数 , 使得;③当时,;④当 , 方程组的解也是方程的解.
A、1 B、2 C、3 D、4二、填空题(本大题共4小题,共16分)
-
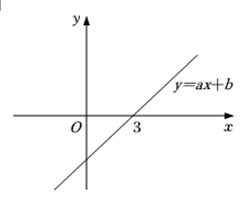
13. 计算:的结果是 .14. 如图,已知函数的图象与轴的交点坐标为 , 则根据图象可得不等式的解集是 .
 15. 如图,已知中, , , 将绕点逆时针反向旋转到的位置,连接 , 则的长为 .
15. 如图,已知中, , , 将绕点逆时针反向旋转到的位置,连接 , 则的长为 . 16. 为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中,甲种粗粮每袋装有3千克粗粮,1千克粗粮,1千克粗粮;乙种粗粮每袋装有1千克粗粮,2千克粗粮,2千克粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中的 , , 三种粗粮的成本价之和.已知粗粮每千克成本价为元,甲种粗粮每袋售价为58.5元,利润率为30%,乙种粗粮的利润率为20%若这两种袋装粗粮的销售利润率达到24%,则该电商销售甲、乙两种袋装粗粮的数量之比是.(商品的利润率)
16. 为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中,甲种粗粮每袋装有3千克粗粮,1千克粗粮,1千克粗粮;乙种粗粮每袋装有1千克粗粮,2千克粗粮,2千克粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中的 , , 三种粗粮的成本价之和.已知粗粮每千克成本价为元,甲种粗粮每袋售价为58.5元,利润率为30%,乙种粗粮的利润率为20%若这两种袋装粗粮的销售利润率达到24%,则该电商销售甲、乙两种袋装粗粮的数量之比是.(商品的利润率)三、解答题(本大题共9小题,共86分。)
-
17. 计算或化简:(1)、;(2)、 .18. 解不等式组或方程:(1)、;(2)、 .19. 如图,在▱中, .
 (1)、用尺规完成以下基本作图:在上截取 , 使;作的平分线交于点(保留作图痕迹,不写作法).(2)、在(1)所作的图形中,连接交于点 , 证明: .20. 有甲、乙两家肉禽类公司到某超市推销鸡腿,两家鸡腿价格相同,品质相似.超市决定通过评估质量来确定选择哪家鸡腿,检查人员从两家分别抽取了100个鸡腿,然后再从中随机各抽取20个,这些鸡腿的质量记为x(单位:克),将所得的数据分为5组(A组: , 组, , 组: , 组: , 组:),学校对数据进行分析后,得到如下部分信息:
(1)、用尺规完成以下基本作图:在上截取 , 使;作的平分线交于点(保留作图痕迹,不写作法).(2)、在(1)所作的图形中,连接交于点 , 证明: .20. 有甲、乙两家肉禽类公司到某超市推销鸡腿,两家鸡腿价格相同,品质相似.超市决定通过评估质量来确定选择哪家鸡腿,检查人员从两家分别抽取了100个鸡腿,然后再从中随机各抽取20个,这些鸡腿的质量记为x(单位:克),将所得的数据分为5组(A组: , 组, , 组: , 组: , 组:),学校对数据进行分析后,得到如下部分信息:甲公司被抽取的20个鸡腿质量频数分布直方图(图1):
乙公司被抽取的20个鸡腿质量扇形统计图(图2):
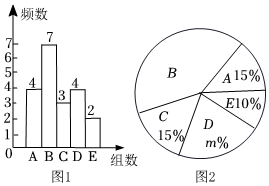
甲公司被抽取的鸡腿质量在这一组的数据是:75,76,78,76,77,78,79.
乙公司被抽取的鸡腿质量在这一组的数据是:75,78,75,75,75,77,76,75.
甲、乙公司被抽取的鸡腿质量的平均数、中位数、众数如下:
公司
甲公司
乙公司
平均数
73
73
中位数
n 75
众数
74
根据以上信息,解答下列问题:
(1)、直接写出上述表中 , , ;(2)、根据以上数据,请估算乙公司这100个鸡腿中质量不低于75克的数量;(3)、根据以上数据分析,如果你是超市采购人员,你会选择采购哪个公司的鸡腿,请说明理由(写出一条理由即可).21. “数形结合百般好”在代数式的学习过程中我们可以结合图形理解相关公式的产生,如图所示的正方形,我们可以利用两种不同的方法计算它的面积,从而得到完全平方公式: .请结合以上知识,解答下列问题:
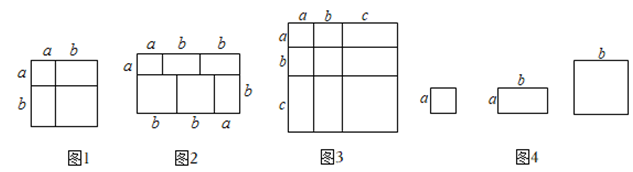 (1)、写出图2所示的长方形所表示的数学等式;(2)、根据图3得到的结论,解决下列问题:
(1)、写出图2所示的长方形所表示的数学等式;(2)、根据图3得到的结论,解决下列问题:若 , , 求代数式的值;
(3)、小明同学用图4中张边长为的正方形纸片,张边长为的正方形纸片,张边长分别为 , 的长方形纸片拼出一个面积为的长方形,求代数式的值.22. 某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵8元,用2400元购买甲种商品的件数恰好与用2000元购买乙种商品的件数相同.(1)、求甲、乙两种商品每件的价格各是多少元?(2)、计划购买这两种商品共80件,且投入的经费不超过3600元,那么最多可购买多少件甲种商品?23. 如果一个自然数的个位数字不为0,且能分解成 , 其中与都是两位数,与的十位数字相同,个位数字之和为10,则称数为“等十数”,并把数分解成的过程,称为“巧拆分”.例如: , 28和22的十位数字相同,个位数字之和为10,是“等十数”.
又如: , 和的十位数字相同,但个位数字之和不等于10,不是“等十数”.
(1)、判断195,624是否是“等十数”?并说明理由;(2)、把一个四位“等十数”进行“巧拆分”,即 , 的各个数位数字之和与的各个数位之和的和记为 , 的各个数位数字之和与的各个数位之和的差的绝对值记为令 , 当能被5整除时,求出所有满足条件的 .24. 如图1,在平面直角坐标系中,点在轴的正半轴上,点 , 轴交轴于点 , .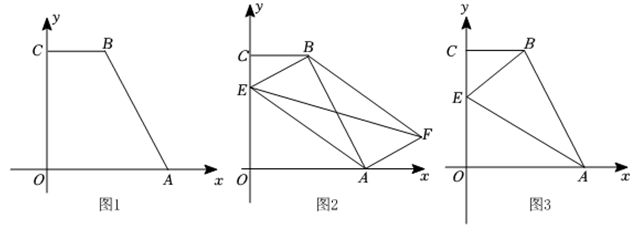 (1)、求点的坐标;(2)、如图2,点是轴上一动点,点为平面内一点,且为▱的对角线,当最小时,请直接写出点的坐标,并在轴上找一点使最大,求出此时点的坐标;(3)、如图3,点仍是轴上一动点,是否存在点使为等腰三角形,请直接写出点的坐标,若不存在,请说明理由.25. 如图1,▱中,于点, , 过点作交于点 .
(1)、求点的坐标;(2)、如图2,点是轴上一动点,点为平面内一点,且为▱的对角线,当最小时,请直接写出点的坐标,并在轴上找一点使最大,求出此时点的坐标;(3)、如图3,点仍是轴上一动点,是否存在点使为等腰三角形,请直接写出点的坐标,若不存在,请说明理由.25. 如图1,▱中,于点, , 过点作交于点 . (1)、若 , , 求的长;(2)、如图2,连接 , 点为线段上一动点,连接 , 将线段绕点逆时针旋转至 , 连接 , 求证:;(3)、在(1)(2)的条件下,点为直线上一点,连接 , 请直接写出的最小值.
(1)、若 , , 求的长;(2)、如图2,连接 , 点为线段上一动点,连接 , 将线段绕点逆时针旋转至 , 连接 , 求证:;(3)、在(1)(2)的条件下,点为直线上一点,连接 , 请直接写出的最小值.