陕西省西安市未央区西航一中2022-2023学年九年级上学期开学数学试卷

试卷更新日期：2022-09-27 类型：开学考试

进入出卷网下载

一、选择题（本题共8小题，共24分）

1. $- 3 \frac{1}{2}$ 的倒数是（）

A、 $\frac{7}{2}$ B、 $\frac{2}{7}$ C、 $- \frac{7}{2}$ D、 $- \frac{2}{7}$

查看试题解析
2. 如图，已知 $A B / / C D$ ，点 $E$ 在线段 $A D$ 上 $($ 不与点 $A$ ，点 $D$ 重合 $)$ ，连接 $C E .$ 若 $∠ C = 20 °$ ， $∠ A E C = 50 °$ ，则 $∠ A =$ （）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
3. 计算 $3 x^{2} \cdot (- 2 x)^{3}$ 的结果是（）

A、 $- 18 x^{5}$ B、 $- 24 x^{5}$ C、 $- 24 x^{6}$ D、 $- 18 x^{6}$

查看试题解析
4. 如图，▱ $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $A B ⊥ A C$ ，若 $A B = 4$ ， $A C = 6$ ，则 $B D$ 的长是（）

A、8 B、9 C、10 D、11

查看试题解析
5. 如图，在 $△ A B C$ 中， $B C = 4$ ，点 $D$ ， $E$ 分别为 $A B$ ， $A C$ 的中点，则 $D E =$ （）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
6. 如图，在平面直角坐标系中，直线 $l_{1}$ ： $y = x + 3$ 与直线 $l_{2}$ ： $y = m x + n$ 交于点 $A (- 1 ， b)$ ，则关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} y = x + 3 \\ y = m x + n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$

查看试题解析
7. 一元二次方程 $y^{2} - y - \frac{3}{4} = 0$ 配方后可化为（）

A、 ${(y + \frac{1}{2})}^{2} = 1$ B、 ${(y - \frac{1}{2})}^{2} = 1$ C、 ${(y + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(y - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
8. 若点 $A (x_{1} ， - 1)$ ， $B (x_{2} ， - 2)$ ， $C (x_{3} ， 3)$ 在一次函数 $y = - 2 x + m$ （ $m$ 是常数）的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} > x_{2} > x_{3}$ B、 $x_{2} > x_{1} > x_{3}$ C、 $x_{1} > x_{3} > x_{2}$ D、 $x_{3} > x_{2} > x_{1}$

查看试题解析

二、填空题（本题共5小题，共15分）

9. 计算； $\sqrt{3} \times$ （ $- \frac{\sqrt{12}}{3}$ ）＝．

查看试题解析
10. 实数 $a$ 、 $b$ 在数轴上的位置如图所示，那么 $\sqrt{(b - a)^{2}} + | b |$ 化简的结果是．

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D$ ， $D E / / A B$ 交 $A C$ 于点 $E$ ，已知 $C E = \sqrt{3}$ ， $C D = 3$ ，则 $A D$ 长为．

查看试题解析
12. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 \sqrt{2} x + k = 0$ 有两个相等的实数根，则 $k$ 的值为．

查看试题解析
13. 已知，如图，四边形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点 $O$ ， $∠ A C D = 22 °$ ， $∠ B D C = 50 °$ ， $∠ B A C = 2 ∠ A B D$ ，则 $∠ B A C$ 的度数为 $° .$

查看试题解析

三、选择题（本题共13小题，共81分）

14. 计算： $(- 1)^{- 3} + \sqrt[3]{8} + | 2 - \sqrt{5} | + (\frac{π}{2} - 1.57)^{0} - \sqrt{20}$ ．

查看试题解析
15. 解不等式组 ${\begin{array}{l} 4 (x + 1) \leq 7 x + 13 \\ x - 4 < \frac{x - 8}{3} \end{array}$ ，并写出它的所有负整数解．

查看试题解析
16. 化简： $(x - \frac{2 x y - y^{2}}{x}) \div \frac{x^{2} - y^{2}}{x^{2} + x y}$

查看试题解析
17. 已知： $R t △ A B C$ ， $∠ B = 90 °$ ．
求作：点 $P$ ，使点 $P$ 在 $△ A B C$ 内部．且 $P B = P C$ ， $∠ P B C = 45 °$ ．

查看试题解析
18. 如图：点 $C$ 、 $D$ 在 $A B$ 上，且 $A C = B D$ ， $A E = F B$ ， $A E / / B F .$ 求证： $D E / / C F$ ．

查看试题解析
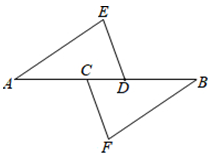19. 在如图所示的直角坐标系中，每个小方格都是边长为1的正方形， $△ A B C$ 的顶点均在格点上，点 $A$ 的坐标是 $(- 3 ， - 1)$ ．

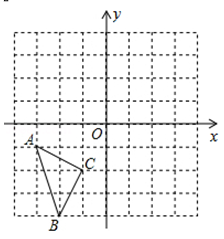(1)、将 $△ A B C$ 沿 $y$ 轴正方向平移3个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 坐标；

(2)、若 $△ A_{2} B_{2} C_{2}$ 与 $△ A_{1} B_{1} C_{1}$ 关于 $y$ 轴对称，写出点 $C_{2}$ 的坐标．

查看试题解析
20. “西安年，最中国” $.$ 西安某校九年级 $1$ 班数学兴趣小组就“最想去的西安市旅游景点”，随机调查了本校部分学生， $A -$ 临潼秦始皇帝陵博物馆 $($ 兵马俑 $)$ ， $B -$ 大唐芙蓉园， $C -$ 西安城墙、 $D -$ 陕西历史博物馆， $E -$ 大雁塔．要求每位同学选择且只能选择一个最想去的景点．下面是根据调查结果进行数据整理后绘制出的不完整统计图，请根据图中信息，解答下列问题：

(1)、补全条形统计图，则扇形统计图中表示最想去景点 $C$ 的扇形圆心角的度数为 ▲ 度；

(2)、所抽取的部分学生的众数落在组内；

(3)、若该校共有1800名学生，请估计最想去景点 $D$ 的学生人数．

查看试题解析
21. 新冠疫情期间，为了提高人民群众防疫意识，很多地方的宣讲车开起来了，大喇叭响起来了，宣传横幅挂起来了，电子屏亮起来了，电视、广播、微信、短信齐上阵，防疫标语、宣传金句频出，这传递着打赢疫情防控阻击战的坚定决心．如图，在一条笔直公路 $M N$ 的一侧点 $A$ 处有一村庄，村庄 $A$ 到公路 $M N$ 的距离 $A B$ 为800米，若宣讲车周围1000米以内能听到广播宣传，宣讲车在公路 $M N$ 上沿 $M N$ 方向行驶．

(1)、请问村庄 $A$ 能否听到宣传？请说明理由；

(2)、如果能听到，已知宣讲车的速度是300米 $/$ 分钟，那么村庄 $A$ 总共能听到多长时间的宣传？

查看试题解析
22. 司机小王开车从 $A$ 地出发去 $B$ 地送信，其行驶路 $s$ 与行驶时间 $t$ 之间的关系如图所示，当汽车行驶若干小时到达 $C$ 地时，汽车发生了故障，需停车检修，修理了几小时后，为了按时赶到 $B$ 地，汽车加快了速度，结果正好按时赶到，根据题意结合图回答下列问题：

(1)、上述问题中反映的是哪两个变量之间的关系？指出自变量和因变量．

(2)、汽车从 $A$ 地到 $C$ 地用了几小时？平均每小时行驶多少千米？

(3)、汽车停车检修了多长时间？车修好后每小时走多少千米？

查看试题解析
23. 已知一个三角形的两边长 $a$ 和 $b$ 满足 $(a - 6)^{2} + \sqrt{b - 4} = 0$ ，第三条边长 $c$ 是方程 $x^{2} - 6 x + 8 = 0$ 的根．

(1)、判断这个三角形的形状；

(2)、求这个三角形面积以及第三边 $c$ 上的高．

查看试题解析

24. 为庆祝中国共产主义青年团成立100周年，学校团委在八、九年级各抽取50名团员开展团知识竞赛，为便于统计成绩，制定了取整数的计分方式，满分10分．竞赛成绩如图所示：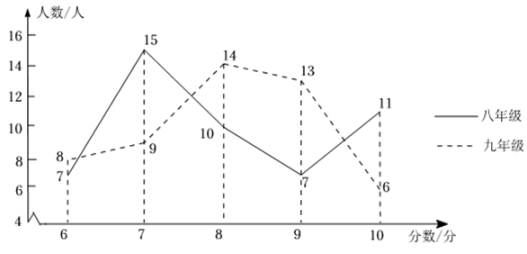

(1)、你能用成绩的平均数判断哪个年级的成绩比较好吗？通过计算说明；

(2)、请根据图表中的信息，回答下列问题．

	众数	中位数	方差
八年级竞赛成绩	7	8	1.88
九年级竞赛成绩	$a$	8	$b$

①表中的 $a =$ ▲ ， $b =$ ▲ ；

②现要给成绩突出的年级颁奖，如果分别从众数和方差两个角度来分析，你认为应该给哪个年级颁奖？

(3)、若规定成绩10分获一等奖，9分获二等奖，8分获三等奖，则哪个年级的获奖率高？

查看试题解析

25. 如图，在▱ $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A B = A D$ ．

(1)、求证： $A C ⊥ B D$ ；

(2)、若点 $E$ ， $F$ 分别为 $A D$ ， $A O$ 的中点，连接 $E F$ ， $E F = \frac{3}{2}$ ， $A O = 2$ ，求 $B D$ 的长及四边形 $A B C D$ 的周长．

查看试题解析
26. 如图①，在平面直角坐标系中，点 $A$ 、 $B$ 的坐标分别为 $(- 1 ， 0)$ 、 $(3 ， 0)$ ，现同时将点 $A$ 、 $B$ 向上平移2个单位长度，再向右平移一个单位长度，得到 $A$ 、 $B$ 的对应点 $C$ 、 $D$ ，连接 $A C$ 、 $B D$ 、 $C D$ ．

(1)、写出点 $C$ 、 $D$ 的坐标并求出四边形 $A B D C$ 的面积；

(2)、在 $x$ 轴上是否存在一点 $F$ ，使得 $△ D F C$ 的面积是 $△ D F B$ 面积的2倍？若存在，请求出点 $F$ 的坐标；若不存在，请说明理由；

(3)、如图②，点 $P$ 是直线 $B D$ 上一个动点，连接 $P C$ 、 $P O$ ，当点 $P$ 在直线 $B D$ 上运动时，请直接写出 $∠ O P C$ 与 $∠ P C D$ 、 $∠ P O B$ 的数量关系．

查看试题解析