河南省郑州七十九中2022-2023学年八年级上学期开学数学试卷

试卷更新日期：2022-09-27 类型：开学考试

进入出卷网下载

一、选择题（共10小题，共30分）.

1. 下列2022年北京冬奥会吉祥物冰墩墩的图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所已研制出直径小于 $0.5 n m$ 的碳纳米管，已知 $1 n m = 0.000000001 m$ ，则将 $0.5 n m$ 用科学记数法表示为（）

A、 $5 \times 1 0^{- 10} m$ B、 $0.5 \times 1 0^{- 9} m$ C、 $5 \times 1 0^{- 8} m$ D、 $5 \times 1 0^{- 9} m$

查看试题解析
3. 下列计算正确的是（）

A、 $(a - b) (- a - b) = a^{2} - b^{2}$ B、 $2 a^{3} + 3 a^{3} = 5 a^{6}$ C、 $6 x^{3} y^{2} \div 3 x = 2 x^{2} y^{2}$ D、 ${(- 2 x^{2})}^{3} = - 6 x^{6}$

查看试题解析
4. 下列事件中，属于不可能事件的是（）

A、掷一枚骰子，朝上一面的点数为5 B、任意画一个三角形，它的内角和是 $178 °$ C、某个数的相反数等于它本身 D、在纸上画两条直线，这两条直线互相垂直

查看试题解析
5. 如图，下列条件中，一定能判断 $A B / / C D$ 的是（）

A、 $∠ 2 = ∠ 3$ B、 $∠ 1 = ∠ 2$ C、 $∠ 4 = ∠ 5$ D、 $∠ 3 = ∠ 4$

查看试题解析
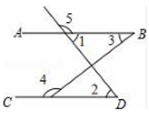6. 下列说法正确的个数有（）
①有两组边对应相等，一组角对应相等的两个三角形全等；②垂直于同一条直线的两直线平行；③三角形的中线把三角形的面积平分；④等腰三角形高所在的直线是对称轴．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 若 $| x + y - 5 | + (x y - 3)^{2} = 0$ ，则 $x^{2} + y^{2}$ 的值为（）

A、19 B、31 C、27 D、23

查看试题解析
8. 如图，从边长为 $a$ 的大正方形中剪掉一个边长为 $b$ 的小正方形，将阴影部分剪下，拼成右边的矩形，由图形①到图形②的变化过程能够验证的一个等式是（）

A、 $a (a + b) = a^{2} + a b$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ D、 $a (a - b) = a^{2} - a b$

查看试题解析
9. 下列各情景分别可以用哪一幅图来近似的刻画？正确的顺序是（）
①汽车紧急刹车（速度与时间的关系）
②人的身高变化（身高与年龄的关系）
③跳过运动员跳跃横杆（高度与时间的关系）
④一面冉冉上升的红旗（高度与时间的关系）

A、 $a b c d$ B、 $d a b c$ C、 $d b c a$ D、 $c a b d$

查看试题解析
10. 如图， $C$ 为线段 $A E$ 上一动点 $($ 不与 $A$ ， $E$ 重合 $)$ ，在 $A E$ 同侧分别作等边 $△ A B C$ 和等边 $△ E C D$ ， $A D$ 与 $B E$ 交于点 $O$ ， $A D$ 与 $B C$ 交于点 $P$ ， $B E$ 与 $C D$ 交于点 $Q$ ，连接 $P Q$ ，则有以下五个结论：
$① A D = B E$ ； $② P Q / / A E$ ； $③ A P = B Q$ ； $④ D E = D P$ ； $⑤ ∠ A O B = 60 °$ ．
其中正确的有（）

A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤

查看试题解析

二、填空题（本题共5小题，共15分）

11. 若 $a^{m} = 8$ ， $a^{n} = 2$ ，则 $a^{m - 3 n}$ 的值是．

查看试题解析
12. 如图， $A E$ 平分 $∠ C A D$ ，点 $B$ 在射线 $A E$ 上，若使 $△ A B C$ ≌ $△ A B D$ ，则还需添加的一个条件是（只填一个即可）．

查看试题解析
13. 七巧板是我国古代劳动人民的发明之一，被誉为“东方魔板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图是一个用七巧板拼成的正方形飞镖游戏板，某人向该游戏板投掷飞镖一次 $($ 假设飞镖落在游戏板上 $)$ ，则飞镖落在阴影部分的概率是．

查看试题解析
14. 直线 $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 表示三条两两相互交叉的公路，现在拟建一个货物中转站，要求它到三条公路的距离都相等，则可供选择的地址有处．

查看试题解析
15. 如图，在等腰 $△ A B C$ 中， $A B = A C$ ， $B C = 8$ ，作 $A D ⊥ B C$ 于点 $D$ ， $A D = \frac{1}{2} A B$ ，点 $E$ 为 $A C$ 边上的中点，点 $P$ 为 $B C$ 上一动点，则 $P A + P E$ 的最小值为．

查看试题解析

三、解答题（本题共7小题，共75分）

16. 按照题意解答：

(1)、计算： $(\frac{1}{5})^{- 1} - (π - 3)^{0} + (- 2^{3}) - 4 \times | - 1 |$ ；

(2)、化简求值： $[(2 x + y) (2 x - y) - (3 x + y) (x - 2 y) - x^{2}] \div (- \frac{1}{2} y)$ ，其中 $x = - 1$ ， $y = 2$ ．

查看试题解析
17. 如图，已知 $∠ M B N$ ，点 $A$ 为射线 $B M$ 上一定点．

(1)、尺规作图：按要求完成下列作图 $($ 不写作法，保留作图痕迹 $)$ ：
①作线段 $B C = B A$ ，点 $C$ 在射线 $B N$ 上；
②作线段 $A B$ 的垂直平分线 $D E$ ，分别交 $A B$ 、 $B C$ 于点 $D$ 、点 $E$ ；

(2)、在（1）的条件下，连接 $A C$ ， $A E$ ，若 $A C = A E$ ，则 $∠ M B N$ 为．

查看试题解析
18. 如图：在正方形网格上有一个 $△ A B C$ ．

⑴画出 $△ A B C$ 关于直线 $M N$ 的对称图形；

⑵ $△ A B C$ 的形状是 ▲ 三角形；

⑶若在 $M N$ 上存在一点 $P$ ，使得 $P A + P C$ 最小，请在图中画出点 $P$ 的位置；

⑷若网格上最小正方形的边长为1，求 $△ A B C$ 的面积．

查看试题解析

19. 数学试验

数学学习小组在学习“用频率估计概率”的数学活动课上，做投掷骰子（质地均匀的正方体）试验，他们共做了 $100$ 次试验，试验的结果如下：

向上点数	1	2	3	4	5	6
出现次数	12	19	15	18	20	$x$

(1)、求表格中

x

的值．

(2)、计算“3点朝上”的频率．

(3)、数学发现
数学学习小组针对数学试验的结果提出结论：“根据试验及

‘

用频率估计概率

’

的知识，这次试验中出现1点朝上的概率是12%”你认为数学学习小组的结论正确吗？并说明理由．

(4)、结论应用
在一个不透明的盒子里，装有40个黑球和若干个白球，它们除颜色外都相同，搅匀后从中任意摸出一个球，记下颜色再把它放回盒子中，不断重复试验，统计结果发现，随着试验次数越来越多，摸到黑球的频率逐渐稳定在0.2左右．据此估计盒子中大约有白球多少个？

查看试题解析

20. 如图， $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B .$ 求证： $E F / / B C$ ，请完成证明过程及理由填写．

证明： $∵ ∠ 1 + ∠ 2 = 180 °$ （已知），

$∠ 2 = ∠ 4$ （    ）

$∴ ∠ 1 + ∠ 4 = 180 °$ （等量代换）．

$∴ A B / /$       ▲      （    ）

$∴ ∠ B =$       ▲      （    ）

$∵ ∠ 3 = ∠ B$ （    ），

$∴ ∠ 3 = ∠ F D H$ （    ）

$∴ E F / / B C$ （    ）

查看试题解析
21. “龟兔赛跑”的故事同学们都非常熟悉，图中的线段 $O D$ 和折线 $O A B C$ 表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

(1)、填空：折线 $O A B C$ 表示赛跑过程中的路程与时间的关系，线段 $O D$ 表示赛跑过程中的路程与时间的关系．赛跑的全程是米．

(2)、兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？

(3)、乌龟用了多少分钟追上了正在睡觉的兔子？

(4)、兔子醒来，以48千米 $/$ 时的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你算算兔子中间停下睡觉用了多少分钟？

查看试题解析
22. 如图

(1)、发现问题
如图1， $△ A C B$ 和 $△ D C E$ 均为等边三角形，当 $△ D C E$ 旋转至点 $A$ ， $D$ ， $E$ 在同一直线上，连接 $B E$ ．

填空：

① $∠ A E B$ 的度数为；

②线段 $A D$ ， $B E$ 之间的数量关系为．

(2)、拓展研究
如图2， $△ A C B$ 和 $△ D C E$ 均为等腰三角形， $∠ A C B = ∠ D C E = 90 °$ ，点 $A$ ， $D$ ， $E$ 三点在同一直线上， $C M$ 为 $△ D C E$ 中 $D E$ 边上的高，连接 $B E$ ，请判断 $∠ A E B$ 的度数及线段 $C M$ ， $A E$ ， $B E$ 之前的数量关系，并说明理由．

(3)、探究发现
图1中的 $△ A C B$ 和 $△ D C E$ ，在 $△ D C E$ 旋转中当点 $A$ ， $D$ ， $E$ 在不同一直线上时，设 $A D$ 与 $B E$ 相交于点 $O$ ，旋转角 $θ (0 ° < θ < 180 °)$ 尝试在图3中探索 $∠ A O E$ 的度数，直接写出结果，不必说明理由．

查看试题解析